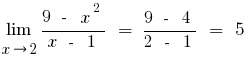
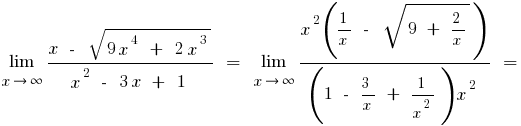
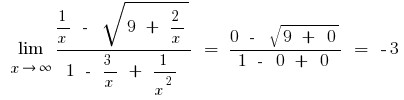
а) пробуємо розкласти чисельник та займенник на множники
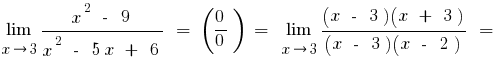
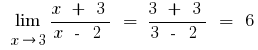
б) якщо до чисельника або знаменника входять вирази з квадратним чи кубічним коренем, то множимо чисельник і знаменник на відповідні вирази, щоб позбутися заданих коренів (іноді вводять заміну і вираз з коренем позначають новою змінною)
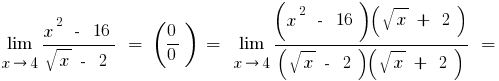
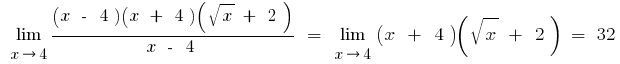
в) якщо під знаком границі стоять тригонометричні або обернені тригонометричні функції, то такі границі зводять до першої визначної границі

або до її варіацій



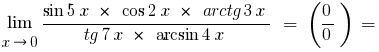
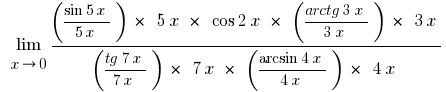
Скоротивши чисельник та знаменник на змінні, що стоять за дужками, враховуючи, що 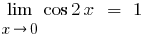 , і враховуючи перщу визначну границю та її варіації, одержуємо
, і враховуючи перщу визначну границю та її варіації, одержуємо 
- Користуючись неперервністю функції
 , пробуємо підставити значення
, пробуємо підставити значення  у функцію
у функцію 
- Якщо обчислюється границя при
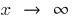 , то пробуємо в чисельнику та займеннику винести за дужки найвищий степінь невідомого
, то пробуємо в чисельнику та займеннику винести за дужки найвищий степінь невідомого - Якщо в результаті підстановки
 одержали вираз типу
одержали вираз типу 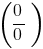 , то
, то

 , пробуємо підставити значення
, пробуємо підставити значення  у функцію
у функцію 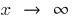 , то пробуємо в чисельнику та займеннику винести за дужки найвищий степінь невідомого
, то пробуємо в чисельнику та займеннику винести за дужки найвищий степінь невідомого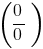 , то
, то