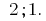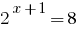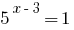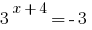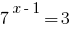Опорні факти
Будь-яка зростаюча (спадна) функція на проміжку набуває кожного свого значення лише в одній точці з цього проміжку.
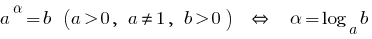
При 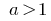 показникова функція
показникова функція  зростає.
зростає.
При  спадає.
спадає.
При 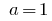 показникова функція
показникова функція  стала.
стала.
Для розвязування показникових рівнянь потрібно добре знати властивості коренів та степенів.
Приклади розвязування найпростіших показникових рівнянь
Розвязування:
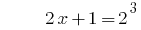
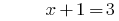
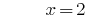
Відповідь: 
Розвязування:
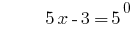
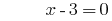
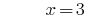
Відповідь: 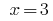
Розвязування:
Коренів немає (оскільки 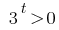 )
)
Відповідь: коренів немає
Розвязування:
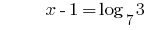
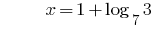
Відповідь: 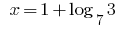
Приклади розвязування показникових рівнянь, зведенням до найпростіших
______________________________________________________________________
Якщо в лівій і правій частинах показникового рівняння стоять тільки добутки, частки, корені ао степені, то доцільно за допомогою основних формул спробувати записати обидві частини рівняння як степені з однією основою.
______________________________________________________________________
Приклад 1:
Розвяжіть рівняння 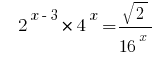 .
.
Розвязання:
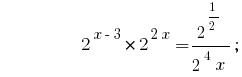
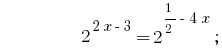
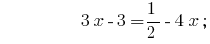
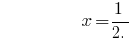
Відповідь: 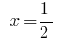 .
.
______________________________________________________________________
Якщо в одній частині показникового рівняння стоїть число, а в іншій усі члени містять вираз виду 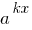 (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь
(показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь  .
.
______________________________________________________________________
Приклад 2:
Розвяжіть рівняння 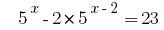 .
.
Розвязання:
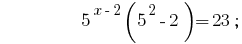
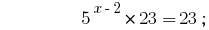
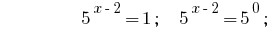
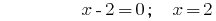
Відповідь: 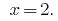 .
.
Приклади розвязування більш складніших показникових рівнянь
______________________________________________________________________
Позбавляємось числових доданків у показниках степенів (використовуючи справа наліво основні властивості степенів).
Якщо можливо, зводимо всі степені до однієї основи і виконуємо заміну змінних.
______________________________________________________________________
Приклад 3:
Розвяжіть рівняння 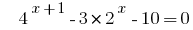 .
.
Розвязання:
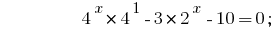
Ураховуючи, що 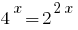 , зводимо степені до однієї основи 2:
, зводимо степені до однієї основи 2: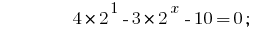
Заміна 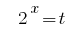 дає рівняння:
дає рівняння:
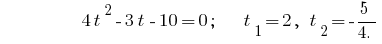
Обернена заміна дає рівняння 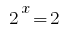 , звідки
, звідки  або
або 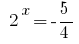 - коренів немає.
- коренів немає.
Відповідь: 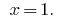
______________________________________________________________________
Якщо не можна звести степені до однієї основи, то пробуємо звести всі степені до двох основ так, щоб одержати однорідне рівняння.
______________________________________________________________________
Приклад 4:
Розвяжіть рівняння 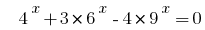 .
.
Розвязання:
Зведемо всі степені до двох основ 2 і 3:
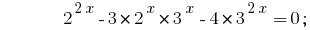
Маємо однорідне рівняння. Для його розвязування поділимо обидві частини на 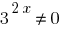 ;
;
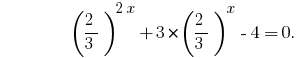
Заміна 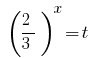 дає рівняння:
дає рівняння:
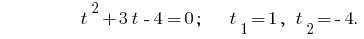
Обернена заміна дає рівняння 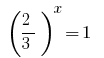 , звідки
, звідки 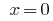 або
або 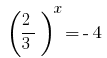 - коренів немає.
- коренів немає.
Відповідь: 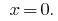
______________________________________________________________________
В інших випадках переносимо всі члени рівняння в одну частину і пробуємо розкласти одержаний вираз на множники або застосовуємо спеціальні прийоми розвязування, у яких використовуємо властивості відповідній функцій.
______________________________________________________________________
Приклад 5:
Розвяжіть рівняння 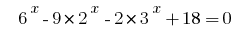 .
.
Розвязання:
Якщо попарно згрупувати члени в лівій частині рівняння і в кожній парі винести за дужки спільний множник, то одержимо :
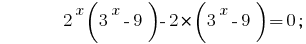
Виносимо за дужки спільний множник 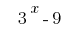 :
:
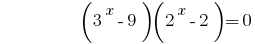
Тоді 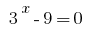 або
або 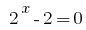 .
.
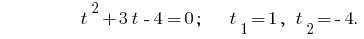
Одержуємо два рівняння 1)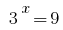 , звідки
, звідки  або 2)
або 2)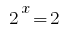 , звідки
, звідки  .
.
Відповідь: