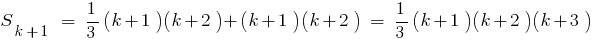Означення: Послідовність —змінна величина, що залежить від натурального числа (тобто функція натурального аргументу).
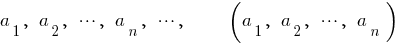 — члени (елементи) послідовності
— члени (елементи) послідовності
Якщо елементи — дійсні числа, то послідовність називається числовою
Приклади
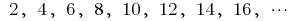 — послідовність парних натуральних чисел
— послідовність парних натуральних чисел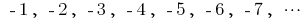 — послідовність цілих відємних чисел
— послідовність цілих відємних чисел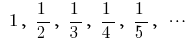 — послідовність чисел, обернених до натуральних
— послідовність чисел, обернених до натуральних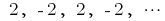 — числова послідовність
— числова послідовність
Зростаючі та спадні послідовності
Означення: Послідовність називається зростаючою, якщо кожний її наступний член більший від попереднього: 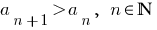 (перша послідовність у прикладах).
(перша послідовність у прикладах).
Означення: Послідовність називається спадною, якщо 
Метод математичної індукції
Вкористовується для доведення тверджень 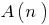 про числові послідовності або про вирази, що залежать від натурального числа, у формулювання яких явно чи неявно присутні слова "для будь-якого натурального
про числові послідовності або про вирази, що залежать від натурального числа, у формулювання яких явно чи неявно присутні слова "для будь-якого натурального  "
"
Схема доведення тверджень за допомогою методу математичної індукції
- Перевіряємо, чи виконується дане твердження при
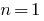 (іноді починають з
(іноді починають з 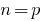 )
) - Припускаємо, що задане твердження справедливе при
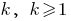 (другий варіант — при
(другий варіант — при 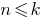 )
) - Доводимо (спираючись на припущення) справедливість нашого твердження і при
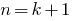
- Робимо висновок, що дане твердження справедливе для будь-якого натурального числа
 (для будь-якого
(для будь-якого 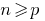 )
)
Приклад.
Довести: 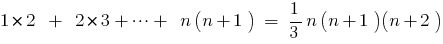
Розвязання. Для зручності запису позначимо 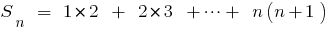
- При
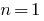 рівність виконується
рівність виконується 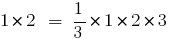
- Припускаємо, що задана рівність правильна при
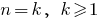 , тобто
, тобто 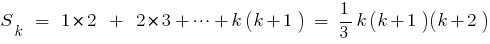
- Доведемо, що рівність виконується і при
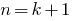 , тобто доведемо, що
, тобто доведемо, що 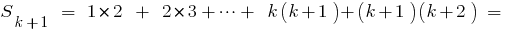
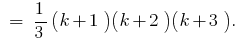
Враховуючи, що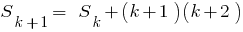 , одержуємо
, одержуємо 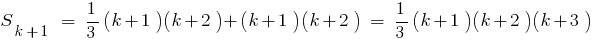
- Отже, задана рівність правильна для будь-якого натурального


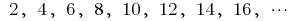 — послідовність парних натуральних чисел
— послідовність парних натуральних чисел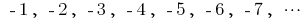 — послідовність цілих відємних чисел
— послідовність цілих відємних чисел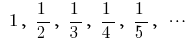 — послідовність чисел, обернених до натуральних
— послідовність чисел, обернених до натуральних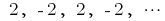 — числова послідовність
— числова послідовність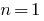 (іноді починають з
(іноді починають з 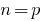 )
)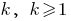 (другий варіант — при
(другий варіант — при 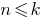 )
)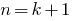
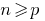 )
)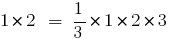
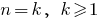 , тобто
, тобто 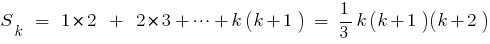
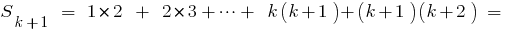
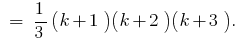
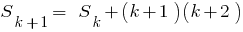 , одержуємо
, одержуємо