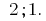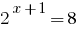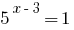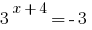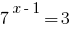Pontos de fatos
Qualquer crescente (primeiro) função no intervalo de cada um adquire o seu valor em um ponto só a partir deste período.
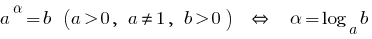
Quando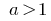 
a função de representante 
aumenta.
Quando vem.
Quando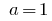 
a função de representante se tornou.
Para resolver equações exponenciais precisa conhecer bem as propriedades das raízes e graus.
Exemplos de solução mais simples de equações exponenciais
Solução:
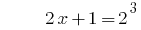
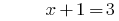
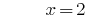
Resposta: 
Solução:
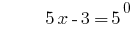
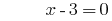
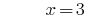
Resposta: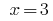 
Solução:
As raízes não (tão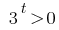 
)
Resposta: as raízes não
Solução:
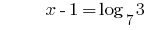
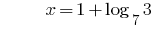
Resposta: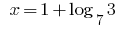 
Exemplos de resolver equações exponenciais a mixagem ao mais simples
______________________________________________________________________
Se nos lados esquerdo e direito exponencial da equação custam apenas obras, a proporção, as raízes ao ponto, que é apropriado usando principais fórmulas tentar escrever a ambas as partes da equação como o grau com uma base.
______________________________________________________________________
Exemplo 1:
Розвяжіть equação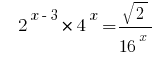 
.
Solução:
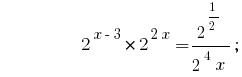
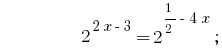
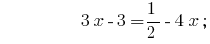
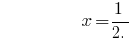
Resposta: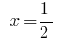 
.
______________________________________________________________________
Se uma parte da exponencial da equação vale a pena, o número e outra com todos os membros contendo uma expressão da forma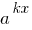 
(indicadores de graus diferem apenas os membros livres), é conveniente a esta parte da equação levado para fora de parênteses menor grau 
.
______________________________________________________________________
Exemplo 2:
Розвяжіть equação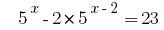 
.
Solução:
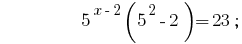
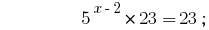
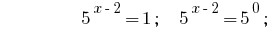
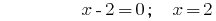
Resposta: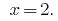 
.
Exemplos de enfrentar os desafios mais complexos de equações exponenciais
______________________________________________________________________
Livrarmo-nos termos numéricos em termos de graus (usando direita para a esquerda, os principais propriedades graus).
Se possível, reduzimos todos os graus de uma base e fazendo a substituição de variáveis.
______________________________________________________________________
Exemplo 3:
Розвяжіть equação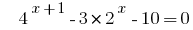 
.
Solução:
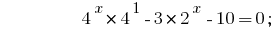
Considerando que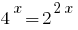 
, redutível a um grau de base 2: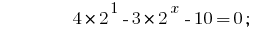
Substituição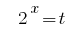 
dá a equação:
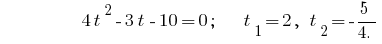
Contrariando a substituição dá a equação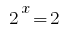 
de onde 
ou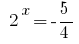 
- raízes não.
Resposta: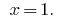 
______________________________________________________________________
Se não medida pode reduzir a uma base, então tentamos minimizar todos os graus de dois fundamentos, de modo a obter homogênea da equação.
______________________________________________________________________
Exemplo 4:
Розвяжіть equação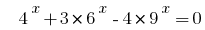 
.
Solução:
Vamos dar todos os graus de dois fundamentos 2 e 3:
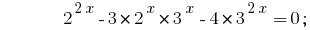
Temos homogênea da equação. Para sua decisão de dividir a ambas as partes em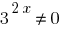 
;
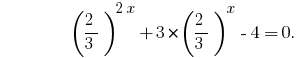
Substituição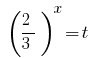 
dá a equação:
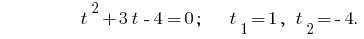
Contrariando a substituição dá a equação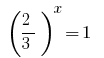 
de onde 
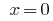ou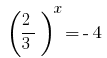 
- raízes não.
Resposta: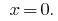 
______________________________________________________________________
Em outros casos, transferimos todos os membros de uma equação em uma parte e tentando decompor recebida a expressão em multiplicadores ou aplicamos técnicas especiais a decisão, em que usamos as propriedades da função correspondente.
______________________________________________________________________
Exemplo 5:
Розвяжіть equação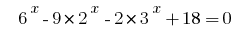 
.
Solução:
Se agrupar em pares de membros, no lado esquerdo da equação e em cada par de ser levado para fora de parênteses multiplicador total, obtemos :
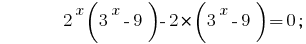
Mantemos fora dos parênteses multiplicador total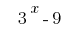 
:
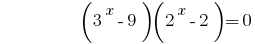
Então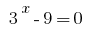 
ou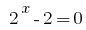 
.
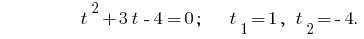
Obtemos duas equações 1)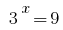
, de onde ou 2)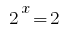 de onde .
Resposta: 