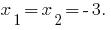第二次方程式，定理韦达

二次方程式

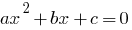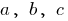定义： 二次方程 —的一个方程式 在哪里 是一号，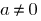

二次方程式一般形式

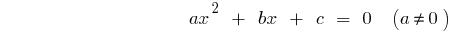
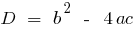— 的判别式的第二次方程式

 

 

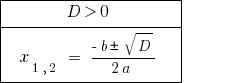
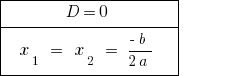
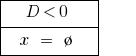
如果 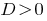该公式有两个明显根源。

如果 该公式有两个平等的根源。 当计数rozwaski被认为是一个值的根源。

在 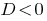方程的根源。

主公式(a=1)

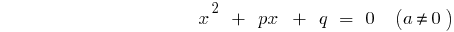
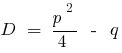— 的判别式的组合式

 

 

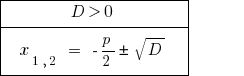
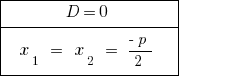
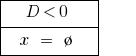
在 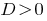主公式有两个明显根源。

当 —公式有两个平等的根源。 当计数rozwaski被认为是一个值的根源。

如果 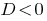—该方程式没有根源。

韦达理在一般情况下

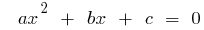如果 根二次方程式 ，然后

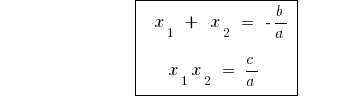
该韦达定理主公式(a=1)

如果 综合的根二次方程式 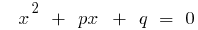，然后

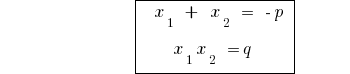
逆定理定理韦达

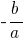定理： 如果总和的两个数 相等 ，该产品仍然 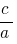，这些数字是根二次方程式 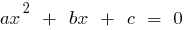的。

 

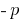理(主公式): 如果这两个数字 相等 ，该产品仍然 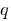，这些数字是根二次方程式 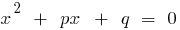的。

 

分解的一个广场三项因素

如果 根二次三项等于零 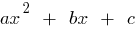(即根源，该公式 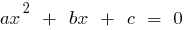)，然后

 

 

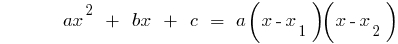
如果判别式方三项等于零(), 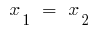然后

 

 

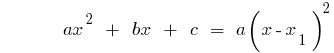
例。 分解的三项上。

1. 时
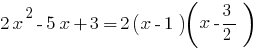
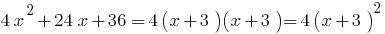
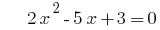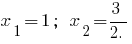
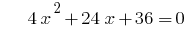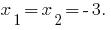
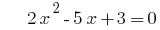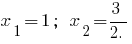
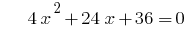2. 时