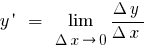
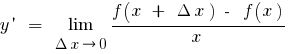
Definition: the Derivative of the function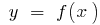 
at the point 
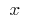is called the limit of the ratio of the increment of the function at point 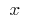to the increment of the argument, when the increment of the argument tends to zero (to denote 
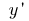or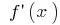 
)
The operation of finding a derivative is called differentiation
The concept of the growth of argument and function
The growth argument
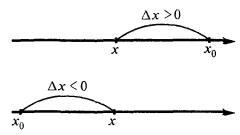
The increment function
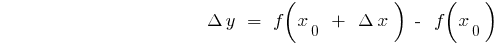
Derivatives of elementary functions
Derivatives of elementary functions are found using the table:
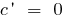
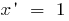
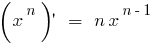
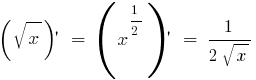
Compiled function. How to find compiled function
Derivative of sum (difference) of two functions, each of which has a derivative equal to the sum (difference) of the derivatives of these functions:
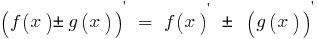
Derivative works of two functions, each of which has a derivative equal to the sum of the products of each function into derivative the second function:
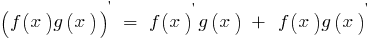
Derivative shares shares of the two functions f(x) and g(x), each of which has derivative g(x)≠0, is given by
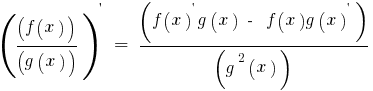
The constant factor can be moved from the sign of the derivative:
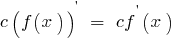
Formulas called rules of differentiation.
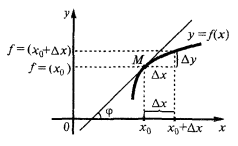
The geometric meaning of derivative
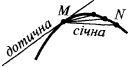
The tangent to the curve at a given point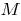 
is called the limiting position of the secant 
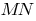, when the point 
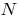is approaching along a curve to the point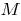
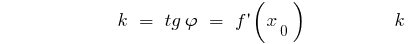— the slope of the tangent
The equation of the tangent to the graph of the function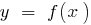 
at the point with Alsou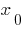 
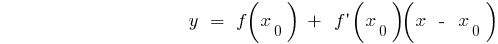
The value of the derivative at the point 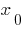is equal to the angular coefficient of the tangent to the graph of the function at the point with Alsou 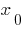and equal to the tangent of the angle of inclination of this tangent to the axis 
Physical meaning of the derivative
The derivative describes the rate of change of the function when you change the argument
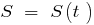— the dependence distance traveled from the time
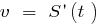— speed rectilinear motion
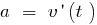— acceleration rectilinear motion