Definición: la Función  se llama periódica con un periodo de
se llama periódica con un periodo de 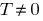 , si alguno
, si alguno  de la zona de determinar el número
de la zona de determinar el número 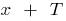 y
y 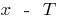 también entran en el ámbito de la definición y
también entran en el ámbito de la definición y
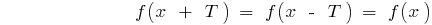 .
.
Propiedades periódicas de la función
- Si el número es
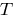 el período de la función
el período de la función  , el número
, el número 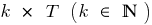 , también es un período en el este de la función.
, también es un período en el este de la función. - Si la función
 periódica con periodo
periódica con periodo 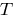 , la función
, la función 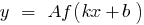 también es periódica y su período es igual a
también es periódica y su período es igual a 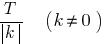
- Si la función
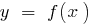 periódica con periodo
periódica con periodo 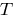 , compuesto de una función (la función de la función)
, compuesto de una función (la función de la función) 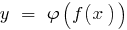 también es periódica con período
también es periódica con período 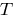 .
. - Para la construcción del gráfico periódica de la función, con un período
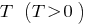 suficiente para construir una curva en el tramo de longitud
suficiente para construir una curva en el tramo de longitud 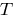 , y luego trasladar paralelamente este gráfico a lo largo del eje
, y luego trasladar paralelamente este gráfico a lo largo del eje 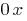 de la distancia
de la distancia 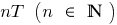 a la izquierda y a la derecha.
a la izquierda y a la derecha.
Ejemplos de funciones periódicas
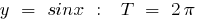
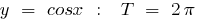
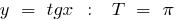
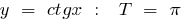

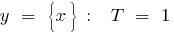
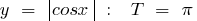
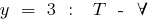

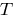 el período de la función
el período de la función 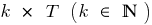 , también es un período en el este de la función.
, también es un período en el este de la función. periódica con periodo
periódica con periodo 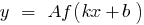 también es periódica y su período es igual a
también es periódica y su período es igual a 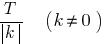
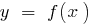 periódica con periodo
periódica con periodo 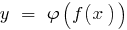 también es periódica con período
también es periódica con período 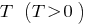 suficiente para construir una curva en el tramo de longitud
suficiente para construir una curva en el tramo de longitud  de la distancia
de la distancia 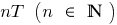 a la izquierda y a la derecha.
a la izquierda y a la derecha.