Схема решению уравнений, замена переменных

Решению уравнений с помощью уравнений-следствий

1. Преобразования, гарантирующие сохранение правильной равенства
2. Проверка корней подстановкой в исходное уравнение

Решению уравнений с помощью равносильных преобразований

1. Учесть ОДЗ правильную равенство при прямых и обратных преобразованиях
2. Сохранять на ОДЗ правильную равенство при прямых и обратных преобразованиях

Решению уравнений. Замена переменных

Если в уравнение переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной).

Пример 1.

Розвяжіть уравнения: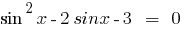

Розвязання.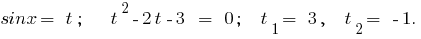

1. При 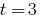уравнение 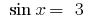корней не имеет, поскольку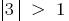

2. При 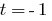имеем 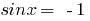, тогда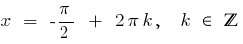

Ответ: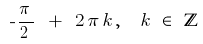

Пример 2.

Розвяжіть уравнения: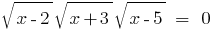

Розвязання. Поскольку под знаком корня парного степеня могут стоять только невідємні выражения, то область допустимых значений (ОДЗ) заданного уравнения задается системой 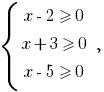розвязком которой является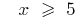

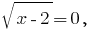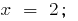
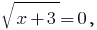Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а все остальные множители существуют: при 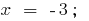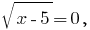при при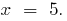

Значение 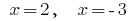не входит в ОДЗ заданного уравнения, следовательно, они не являются корнями заданного уравнения.

Значение 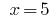входит в ОДЗ, значит, 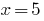является корнем заданного уравнения.

Ответ: