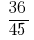С помощью основного свойства дроби можно заменить данный дробь другим, равным данному, но с меньшим числителем и знаменателем. Такая замена называется сокращением дроби.
Чтобы сократить дробь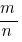 
нужно найти наибольший общий делитель его числителя и знаменателя: НОД (m,n), после чего поделить числитель и знаменатель дроби на это число. Если НОД (m,n)=1, то дробь сократить невозможно.
Примеры сокращения дробей
Пример 1: Сократите дробь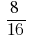 
Решения: НОД (8;16) = 8, тогда
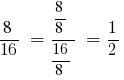
Пример 2: Сократите дробь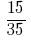 
Решения: НОД (5;35) = 5, тогда
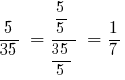
Пример 3: Сократите дробь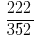 
Решения: НОД (222;352) = 2, тогда
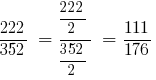
Пример 4: Сократите дробь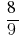 
Решения: НОД (8;9) = 1, тогда по определению дробь сократить невозможно.
Возведение дробей к общему знаменателю
Дроби сводят до наименьшего общего знаменателя. Он равен наименьшему общему кратному (НОК) знаменателей данных дробей, то есть наименьшее число, которое делится на знаменатель первой и второй дроби.
Возведение дробей примеры
Пример 1: привести к общему знаменателю дроби: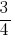 
и
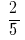
НСК (4, 5) = 20.
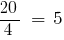— вспомогательный множитель первой дроби,
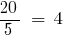— вспомогательный множитель второй дроби.
Тогда:
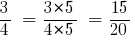
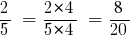
Ответ: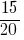 
и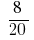 
Пример 2: Свести к общему знаменателю дроб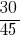и: 
и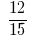
НСК (45, 15) = 45.
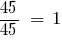— вспомогательный множитель первой дроби,
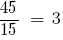— вспомогательный множитель второй дроби.
Тогда:
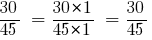
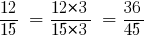
Ответ: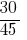 
и