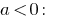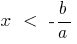线性方程
定义: 线性方程的一个变量  —一个方程式
—一个方程式 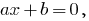 在哪里
在哪里 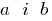 是一个真正的数量。
是一个真正的数量。
如果 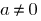 ,然后直线公式也被称为 程的第一学位的。
,然后直线公式也被称为 程的第一学位的。
例的解决线性方程
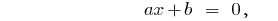 然后
然后 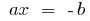
当 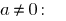
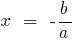 是唯一根
是唯一根
如果 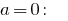
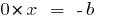 (
(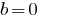
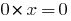 无限数量的根源)
无限数量的根源)
线性不等式
定义: 线性不平等现象在一个变量  是一个不平等的形式
是一个不平等的形式 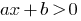 在那里
在那里 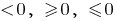 是一个真正的数量。
是一个真正的数量。
如果 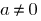 是,nerst也被称为线性 不平等现象的第一学位的。
是,nerst也被称为线性 不平等现象的第一学位的。
例的解决线性不等式
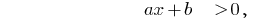 然后
然后 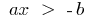
时 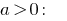
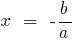
当 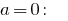
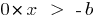 (如果
(如果 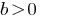 —
—  任何数量
任何数量 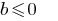 —rozvytku没有。
—rozvytku没有。  任何数量。)
任何数量。)
时