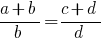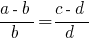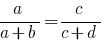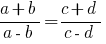定义: 一比例 是相等的两个关系。
 或
或 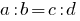 .
.
主要财产的比例
产品中的极端成员的成员的比例是等于其平均名成员组成:如果
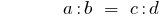 然后
然后 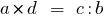
属性的比例
- 产品中的极端成员的成员的比例是等于其平均成员
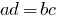 的。
的。 - 一个极端成员的比例是等于其平均成员,除其他极端件。
- 在每个方面都比可以换或只是平均或极成员,或那些与他人同时进行。
一个例子找到一个比例,在数学
如果 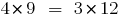 中,
中, 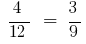
在比例 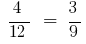 ,以改变地方的平均成员或结束的成员,然后再次获得正确的平等:
,以改变地方的平均成员或结束的成员,然后再次获得正确的平等:
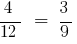 和
和 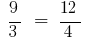
衍生物的比例
如果指定的比例 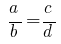 中,
中, 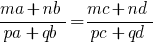 这一比例是被称为衍生物。
这一比例是被称为衍生物。
最经常使用的衍生物的比例
规模
定义: 规模 比的距离地图上的相应的距离上的实际地形。
直接成比例的幅度
定义: 两个数量是所谓的 直接成比例,如果增加值中的一个他们中的好几倍的价值的其他增加的相同因素。
任务直接成比例的幅度
边平方等于3。 如何改变的周边的平方,如果其侧增加3次,4次、5次?
一方面3米,周边12DM
边的平方,DM9,DM36周边
平方面12米,周边48DM
方侧15DM、60周边DM
如果你增加边的广场3倍(3DM、9DM),周边也增加了3倍(DM9,DM36)上。
同样,如果你增加的两侧平的4倍(米3,12个DM),周边也增加了4倍(12DM,DM48).
结论:如果你增加边的广场几次,外围增加相同的因素。
边的平方是直接成比例的其周边。
成反比,数量级
定义: 两个量被称为 比例日式,如果增加值中的一个他们中的好几倍的价值的其他减少通过同样的因素。
任务是成反比,数量级
之间的距离两个小镇是160公里。 需要多少时间从一个村庄到另一个,如果速度10公里/小时增加了2倍,4次,8次呢?
速公里/小时10时,h16
速公里/小时20时,h8
速公里/小时40时,h4
速公里/小时80次,h2
作为速度增加了2倍(10公里/小时,20公里/小时)时间减少(减少)的2倍(16h、8h)。
同样,作为速度增加了4倍(10公里/小时,40公里/小时)时间减少(减少)的4倍(16h、4h)。
结论:为的速度增加好几倍,时间减少通过同样的因素。
速度是成反比的时间。
人数 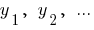 成正比的数字,
成正比的数字, 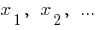 如果
如果 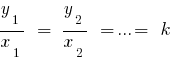 — 的系数相称的。
— 的系数相称的。

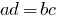 的。
的。