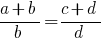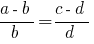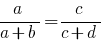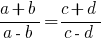Definition: a Proportion is the equality of two relations.
or 
.
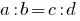The main property of proportions
The product of the extreme members of the members of the proportion is equal to the product of its average members: if
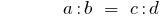then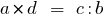 
Properties of proportions
- The product of the extreme members of the members of the proportion is equal to the product of its average members
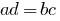. - One extreme member of the proportion is equal to the product of its average members, divided by the other extreme member.
- In every aspect ratio can be swapped or just average or extreme members, or those and others simultaneously.
.An example of finding a ratio in mathematics
If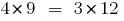 
, 
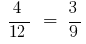
In proportion 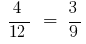to change in places the average members or the end members, then again obtain correct equality:
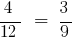and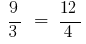 
Derivatives of proportion
If the specified proportion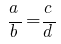 
, 
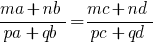that proportion is called the derivative.
The most frequently used derivatives of proportion
Scale
Definition: the Scale — ratio of distance on map to the corresponding distance on the actual terrain.
Directly proportional to the magnitude
Definition: Two quantities are called directly proportional, if the increase in the values of one of them several times the value of the other increases by the same factor.
Tasks directly proportional to the magnitude
Side of the square equal to 3. How to change the perimeter of a square if its side to increase 3 times, 4 times, 5 times?
A square of side 3 DM, perimeter 12 DM
Side of the square, DM 9, DM 36 perimeter
Square side 12 DM, perimeter 48 DM
Square side 15 DM, 60 DM perimeter
If you increase the sides of the square 3 times (was 3 DM, 9 DM), the perimeter also increased 3 times (was DM 9, DM 36).
Similarly, if you increase the sides of the square 4 times (was DM 3, 12 DM), the perimeter also increased 4 times (was 12 DM, DM 48).
Conclusion: if you increase the sides of the square several times, the perimeter increases by the same factor.
Side of the square is directly proportional to its perimeter.
Inversely proportional to the magnitude
Definition: Two quantities are called proportional obento, if increasing values of one of them several times the value of the other decreases by the same factor.
Tasks is inversely proportional to the magnitude
The distance between two towns is 160 km. how much time it takes to get from one village to another, if the speed 10 km/h increase by 2 times, 4 times, 8 times?
Speed km/h 10 time, h 16
Speed km/h 20 time, h 8
Speed km/h 40 time, h 4
Speed km/h 80 time, h 2
As the speed increases 2 times (was 10 km/h, 20 km/h) time reduced (decreased) to 2 times (16 h, 8 h).
Similarly, as the speed increases 4 times (was 10 km/h, 40 km/h) time reduced (decreased) 4 times (16 h, 4 h).
Conclusion: as the speed increases several times, the time decreases by the same factor.
The speed is inversely proportional to time.
Numbers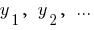 
proportional to the numbers 
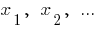if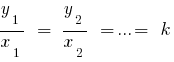 
— the coefficient of proportionality.
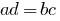