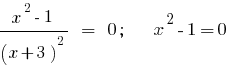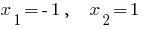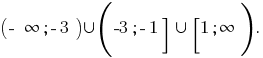Solving inequalities using equivalent transformations
- Conversion, guaranteeing the preservation of the right of equality
- Checking the roots by substitution into the original inequality
Solving equations using the method of intervals
- Find odz.
- Find the zeros of the function:
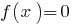
- Note the zeros at DHS and find the sign of the function f(x) in each interval, which split the DHS.
- Record the response given the sign of the given inequality.
The solution of inequalities. The method of intervals.
- Find odz.
- Find the zeros of the function:
- Note the zeros at DHS and find the sign of the function f(x) in each interval, which split the DHS.
- Record the response given the sign of the given inequality.
Example 1.
Rozwarte inequality: 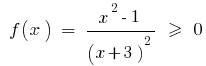
Rozwiazania. Let 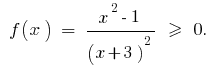
- DHS:
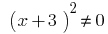 therefore
therefore 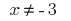 .
. - The zeros of the function:
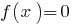
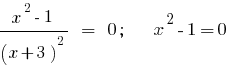
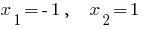
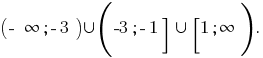
Example 2.
Indicate the smallest integer that is rozvyazka bumps
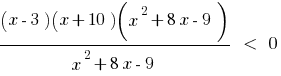
Rozwiazania. Solve this inequality by the method of intervals.
DHS: 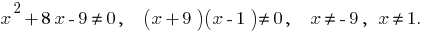
Find the zeros of the function: 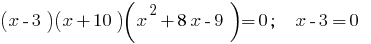 or
or 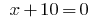
Then 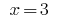 or
or 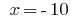 .
.
Depicted zeros and DHS and find a sign function on each interval.
Then, the solution to this inequality 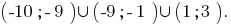 Therefore, the smallest integer that is rozvyazka this inequality is the number
Therefore, the smallest integer that is rozvyazka this inequality is the number 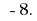
Answer: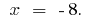

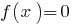
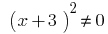 therefore
therefore 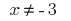 .
.