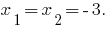The quadratic equation, the theorem of vieta

Quadratic equations

Definition: quadratic equation 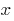— an equation of the form 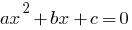where 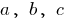is some number, and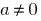

Quadratic equation General form

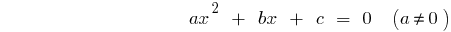
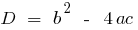— the discriminants of the quadratic equation

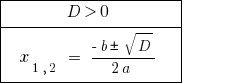
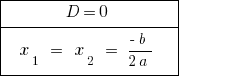
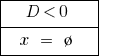
If 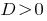the equation has two distinct roots.

If 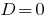the equation has two equal roots. When counting the number rozwaski is considered one value of the root.

When 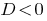— equation roots there.

Master equation (a = 1)

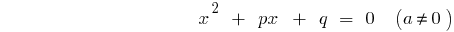
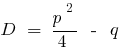— the discriminants of the combined equation

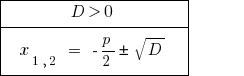
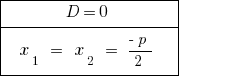
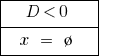
At 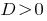— master equation has two distinct roots.

When 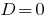— the equation has two equal roots. When counting the number rozwaski is considered one value of the root.

If 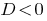— the equations do not have roots.

Vieta theorem in the General case

If 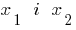the roots of the quadratic equation 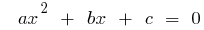, then

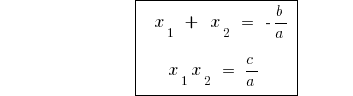
The vieta theorem for the master equation (a=1)

If 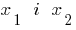the consolidated roots of the quadratic equation 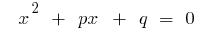, then

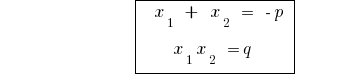
The inverse theorem the theorem of vieta

Theorem: If the sum of the two numbers 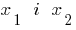equal 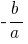, and the product still 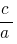, these numbers are roots of the quadratic equation .

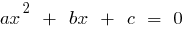Theorem (master equation): If the sum of the two numbers 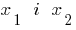equal 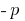, and the product still 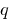, these numbers are roots of the quadratic equation .

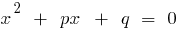Decomposition of a square trinomial into factors

If 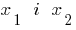the roots of the quadratic trinomial equal to zero 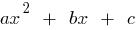(i.e. the roots of the equatio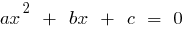n )then

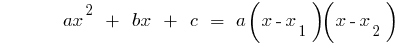
If the discriminants square trinomial is equal to zero (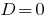), 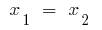and then

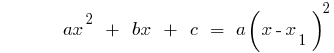
Example. Decomposition of the trinomial.

1. when



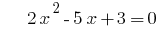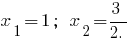
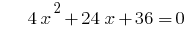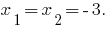
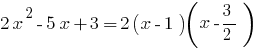
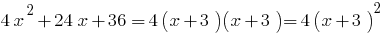
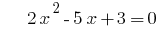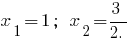
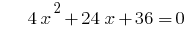2. when