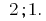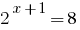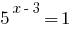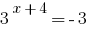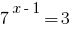Supporting facts
Any increasing (decreasing) function between each acquires its value only in one point of this period.
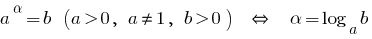
When 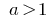 the exponential function
the exponential function 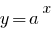 is increasing.
is increasing.
When 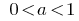 the exponential function
the exponential function 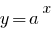 comes in.
comes in.
When 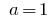 the exponential function
the exponential function 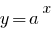 was.
was.
The decision model equations one must know the properties of roots and degrees.
Examples of solution of simple exponential equations
Solution:
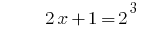
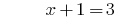
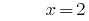
Answer: 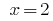
Solution:
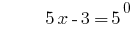
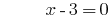
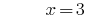
Answer: 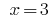
Solution:
No roots (so 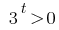 )
)
Answer: no roots
Solution:
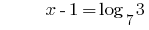
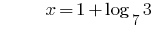
Answer: 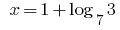
Examples of the solution of model equations by reduction to the simplest
______________________________________________________________________
If the left and right parts of the equations are illustrative only of the work, fractions, roots AO extent, it is advisable using basic formulas to try to record both parts of the equation as powers of one base.
______________________________________________________________________
Example 1:
Rozwarte equations 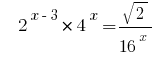 .
.
Solutions:
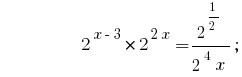
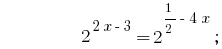
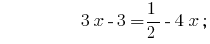
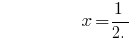
Answer: 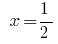 .
.
______________________________________________________________________
If one part of the exponential equation is a number and the other containing all the members of the expression 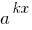 (exponents differ only by free members), it is convenient in this part of the equation to put aside the smallest degree
(exponents differ only by free members), it is convenient in this part of the equation to put aside the smallest degree 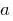 .
.
______________________________________________________________________
Example 2:
Rozwarte equations 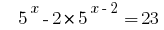 .
.
Solutions:
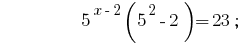
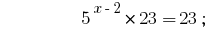
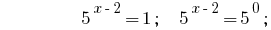
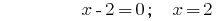
Answer: 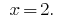 .
.
Examples of more complex exponential equations
______________________________________________________________________
Get rid of numeric terms in the exponents (using right-to-left basic properties of degrees).
If possible, reduce all degrees to one basis and perform a change of variables.
______________________________________________________________________
Example 3:
Rozwarte equations 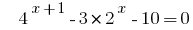 .
.
Solutions:
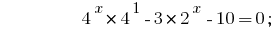
Given that 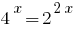 , we reduce the degree by one base 2:
, we reduce the degree by one base 2: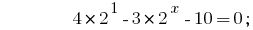
Substitution 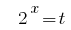 gives the equation:
gives the equation:
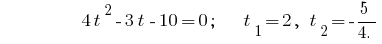
Backward substitution gives the equation 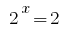 , where
, where 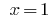 or
or 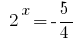 - no roots.
- no roots.
Answer: 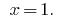
______________________________________________________________________
If not degree can be reduced to one basis, try to reduce all degrees to two bases so as to obtain a homogeneous equation.
______________________________________________________________________
Example 4:
Rozwarte equations 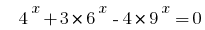 .
.
Solutions:
Let's give all the extent to the two bases 2 and 3:
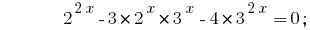
Have a homogeneous equation. For its solution divide both sides by 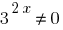 ;
;
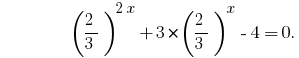
Substitution 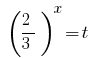 gives the equation:
gives the equation:
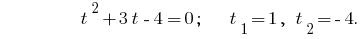
Backward substitution gives the equation 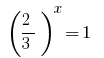 , where
, where 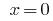 or
or 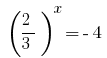 - no roots.
- no roots.
Answer: 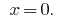
______________________________________________________________________
In other cases, we transfer all the terms in the equation into one part and try to decompose the obtained expression into factors, or apply special techniques to the solution in which we use properties of the corresponding functions.
______________________________________________________________________
Example 5:
Rozwarte equations 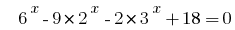 .
.
Solutions:
If in pairs to group members in the left side of the equation, and in each pair stand out a common factor, we get :
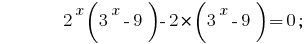
Make the brackets a common factor 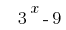 :
:
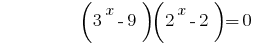
Then 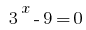 or
or 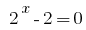 .
.
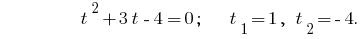
We get two equations 1)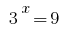 where
where 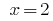 2)
2)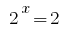 where
where 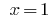 .
.
Answer: