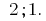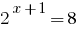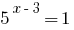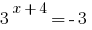Опорные факты
Любая возрастающая (убывающая) функция на промежутке каждого приобретает свое значение только в одной точке из этого промежутка.
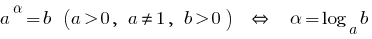
При 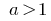 показательная функция
показательная функция  возрастает.
возрастает.
При 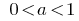 показательная функция
показательная функция  приходит.
приходит.
При 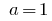 показательная функция
показательная функция  стала.
стала.
По решению показательных уравнений нужно хорошо знать свойства корней и степеней.
Примеры решению простейших показательных уравнений
Решению:
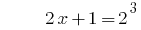
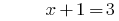
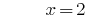
Ответ: 
Решению:
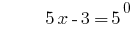
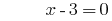
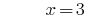
Ответ: 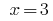
Решению:
Корней нет (так 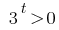 )
)
Ответ: корней нет
Решению:
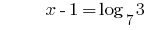
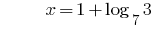
Ответ: 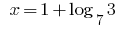
Примеры решению показательных уравнений сведением к простейшим
______________________________________________________________________
Если в левой и правой частях показательного уравнения стоят только произведения, доли, корни ао степени, то целесообразно с помощью основных формул попробовать записать обе части уравнения как степени с одним основанием.
______________________________________________________________________
Пример 1:
Розвяжіть уравнения 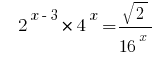 .
.
Решения:
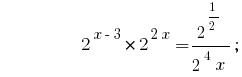
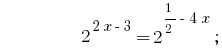
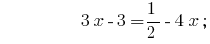
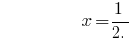
Ответ: 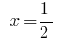 .
.
______________________________________________________________________
Если в одной части показательного уравнения стоит число, а в другой все члены содержащих выражение вида 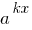 (показатели степеней отличаются только свободными членами), то удобно в этой части уравнения вынести за скобки самый маленький степень
(показатели степеней отличаются только свободными членами), то удобно в этой части уравнения вынести за скобки самый маленький степень  .
.
______________________________________________________________________
Пример 2:
Розвяжіть уравнения 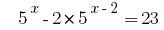 .
.
Решения:
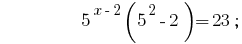
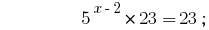
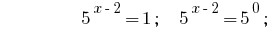
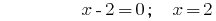
Ответ: 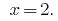 .
.
Примеры решению более сложных показательных уравнений
______________________________________________________________________
Избавляемся от числовых слагаемых в показателях степеней (используя справа налево основные свойства степеней).
Если возможно, сводим все степени к одному основанию и выполняем замену переменных.
______________________________________________________________________
Пример 3:
Розвяжіть уравнения 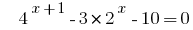 .
.
Решения:
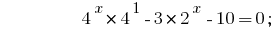
Учитывая, что 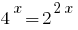 , сводим степени к одному основанию 2:
, сводим степени к одному основанию 2: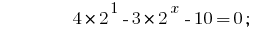
Замена 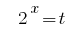 дает уравнение:
дает уравнение:
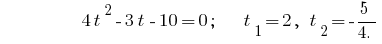
Обратная замена дает уравнение 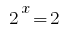 , откуда
, откуда  или
или 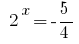 - корней нет.
- корней нет.
Ответ: 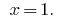
______________________________________________________________________
Если не степени можно свести к одной основе, то пробуем свести все степени к двум основ так, чтобы получить однородное уравнение.
______________________________________________________________________
Пример 4:
Розвяжіть уравнения 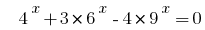 .
.
Решения:
Давайте приведем все степени к двум основ 2 и 3:
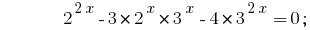
Имеем однородное уравнение. Для его решению поделим обе части на 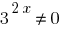 ;
;
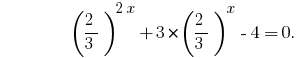
Замена 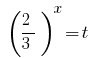 дает уравнение:
дает уравнение:
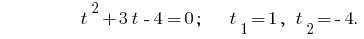
Обратная замена дает уравнение 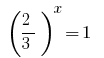 , откуда
, откуда 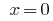 или
или 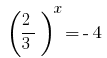 - корней нет.
- корней нет.
Ответ: 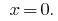
______________________________________________________________________
В других случаях переносим все члены уравнения в одну часть и пробуем разложить полученное выражение на множители или применяем специальные приемы решению, в которых используем свойства соответствующей функции.
______________________________________________________________________
Пример 5:
Розвяжіть уравнения 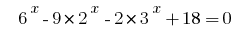 .
.
Решения:
Если попарно сгруппировать члены в левой части уравнения и в каждой паре вынести за скобки общий множитель, то получим :
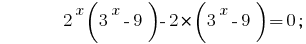
Выносим за скобки общий множитель 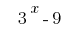 :
:
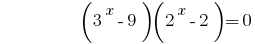
Тогда 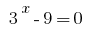 или
или 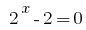 .
.
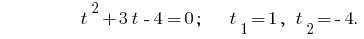
Получаем два уравнения 1)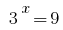 , откуда
, откуда  или 2)
или 2)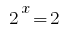 , откуда
, откуда  .
.
Ответ: