Непрерывность функции в точке
Определение: Функция  называется непрерывной в точке
называется непрерывной в точке 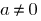 , если при
, если при 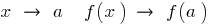 , то есть
, то есть 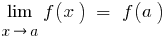 .
.
Непрерывность функции на промежутке
Определение: Если функция  непрерывна в каждой точке некоторого промежутка
непрерывна в каждой точке некоторого промежутка  , то ее называют непрерывной на промежутке
, то ее называют непрерывной на промежутке  .
.
Свойства непрерывности функции
- Если непрерывная на відрузку
 видуальные приобретает на концах этого отрезка значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю.
видуальные приобретает на концах этого отрезка значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. - Если на интервале
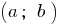 функция
функция  непрерывна и не превращается в ноль, то на этом интервале функция сохраняет постоянный знак.
непрерывна и не превращается в ноль, то на этом интервале функция сохраняет постоянный знак. - Функция
 , непрерывная на отрезке
, непрерывная на отрезке  , принимает всех промежуточных значений между значениями этой функции в крайних точках, то есть между
, принимает всех промежуточных значений между значениями этой функции в крайних точках, то есть между 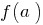 и
и 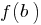 .
. - Функция
 , непрерывная на отрезке
, непрерывная на отрезке  , ограничена на этом отрезке, то есть существуют два числа
, ограничена на этом отрезке, то есть существуют два числа  и
и  , что для всех
, что для всех 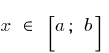 выполняется неравенство
выполняется неравенство 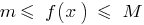 .
. - Сумма разности и произведение непрерывных на данном интервале функций — непрерывная на том же самом интервале функция. Частное двух непрерывных функций — непрерывная функция во всех точках, в которых знаменатель не перетвоюється на ноль.
- Функция, обратная к непрерывной функции на заданном интервале, является непрерывной на этом интервале.
- Если функция
 имеет производную в точке
имеет производную в точке  , то она является непрерывной в этой точке.
, то она является непрерывной в этой точке.
Пример непрерывности функции
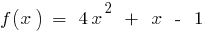 — непрерывная функция (многочлен)
— непрерывная функция (многочлен)
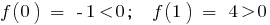 , поэтому на интервале (0;1) существует точка
, поэтому на интервале (0;1) существует точка  , в которой функция равна 0:
, в которой функция равна 0: 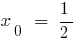
Пример непрерывности функции
Пример непрерывности функции
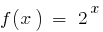 — непрерывная функция. Если
— непрерывная функция. Если
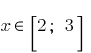 , то
, то 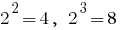 . Поскольку
. Поскольку 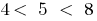 , то существует точка
, то существует точка  , в которой
, в которой 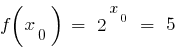 .
.
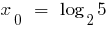
Правило нахождения наибольшего и наименьшего значенб функции.
Точки разрыва
Определение: Точка  точка разрыва функции
точка разрыва функции 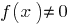 , если в точке
, если в точке  не выполняется условие, что при
не выполняется условие, что при 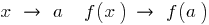 .
.
Примеры функций, содержащих точки разрыва
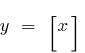 — точки разрыва все целочисленные точки
— точки разрыва все целочисленные точки
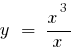 — точка разрыва - 0
— точка разрыва - 0
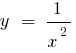 — точка разрыва - 0
— точка разрыва - 0

 видуальные приобретает на концах этого отрезка значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю.
видуальные приобретает на концах этого отрезка значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю.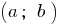 функция
функция 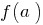 и
и 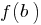 .
. и
и  , что для всех
, что для всех 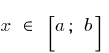 выполняется неравенство
выполняется неравенство 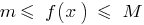 .
.