এর ধারাবাহিকতা ফাংশন সময়ে
সংজ্ঞা: একটি ফাংশন  বলা হয়, একটানা এ
বলা হয়, একটানা এ 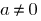 যদি
যদি 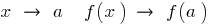 , যে হয়
, যে হয় 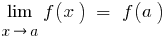 .
.
একটানা ফাংশন ব্যবধান
সংজ্ঞা: যদি একটি ফাংশন হয়,  ক্রমাগত প্রতিটি সময়ে কিছু ব্যবধান
ক্রমাগত প্রতিটি সময়ে কিছু ব্যবধান  , এটা বলা হয়, একটানা ব্যবধান
, এটা বলা হয়, একটানা ব্যবধান  .
.
ধারাবাহিকতা বৈশিষ্ট্য ফাংশন
উদাহরণ ধারাবাহিকতা একটি ফাংশন
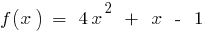 একটি অবিচ্ছিন্ন ফাংশন (polynomial)
একটি অবিচ্ছিন্ন ফাংশন (polynomial)
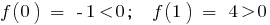 তাই ব্যবধান (0;1) একটি বিন্দু আছে
তাই ব্যবধান (0;1) একটি বিন্দু আছে  যেখানে, ফাংশন, 0 সমান:
যেখানে, ফাংশন, 0 সমান: 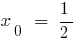
উদাহরণ ধারাবাহিকতা একটি ফাংশন
উদাহরণ ধারাবাহিকতা একটি ফাংশন
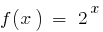 একটি অবিচ্ছিন্ন ফাংশন. যদি
একটি অবিচ্ছিন্ন ফাংশন. যদি
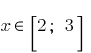 তারপর
তারপর 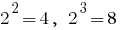 . কারণ
. কারণ 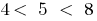 , সেখানে একটি বিন্দু
, সেখানে একটি বিন্দু  যেখানে
যেখানে 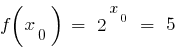 .
.
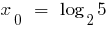
নিয়ম খুঁজে বের বৃহত্তম এবং ক্ষুদ্রতম snakeb ফাংশন.
- যদি একটানা উপর wtrysku
 পৃথক অর্জন শেষ সময়ে এই সেগমেন্ট মান বিভিন্ন লক্ষণ, তারপর কিছু সময়ে এই সেগমেন্ট, তিনি একটি মান শূন্য.
পৃথক অর্জন শেষ সময়ে এই সেগমেন্ট মান বিভিন্ন লক্ষণ, তারপর কিছু সময়ে এই সেগমেন্ট, তিনি একটি মান শূন্য. - যদি ব্যবধান
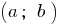 ফাংশন হয়,
ফাংশন হয়,  ক্রমাগত এবং না মধ্যে চালু শূন্য এই ব্যবধান ফাংশন রাখে একটি ধ্রুবক চিহ্ন.
ক্রমাগত এবং না মধ্যে চালু শূন্য এই ব্যবধান ফাংশন রাখে একটি ধ্রুবক চিহ্ন. - একটি ফাংশন
 , ক্রমাগত একটি ব্যবধান
, ক্রমাগত একটি ব্যবধান  লাগে সব অন্তর্বর্তী মান, মানের মধ্যে এই ফাংশন এ চরম পয়েন্ট, অর্থাত্ মধ্যে
লাগে সব অন্তর্বর্তী মান, মানের মধ্যে এই ফাংশন এ চরম পয়েন্ট, অর্থাত্ মধ্যে 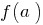 এবং
এবং 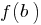 .
. - একটি ফাংশন
 ক্রমাগত একটি সেগমেন্ট
ক্রমাগত একটি সেগমেন্ট  , সীমিত হয়, এই সেগমেন্ট, তারপর সেখানে উপস্থিত দুই নম্বর
, সীমিত হয়, এই সেগমেন্ট, তারপর সেখানে উপস্থিত দুই নম্বর  এবং
এবং  যে জন্য সব
যে জন্য সব 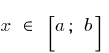 বৈষম্য
বৈষম্য 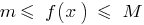 .
. - এর পরিমাণ পার্থক্য, এবং এই কাজ করা হয়, ক্রমাগত এই ব্যবধান ফাংশন একটানা একই ব্যবধান ফাংশন. এই ভাগফল দুই একটানা ফাংশন একটি অবিচ্ছিন্ন ফাংশন এ সব পয়েন্ট যেখানে হর নয় peretolchina শূন্য.
- বিপরীত, একটি অবিচ্ছিন্ন ফাংশন উপর প্রদত্ত ব্যবধান - ক্রমাগত এই ব্যবধান.
- যদি ফাংশন
 আছে একটি অমৌলিক, এ
আছে একটি অমৌলিক, এ  , তারপর, এটা ক্রমাগত যে সময়ে.
, তারপর, এটা ক্রমাগত যে সময়ে.
বিরতি বিন্দু
সংজ্ঞা: বিন্দু  বিরতি বিন্দু ফাংশন
বিরতি বিন্দু ফাংশন 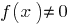 যদি বিন্দু
যদি বিন্দু  নয়, এই শর্তে যে যখন
নয়, এই শর্তে যে যখন 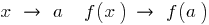 .
.
উদাহরণ ফাংশন সঙ্গে বিরতি পয়েন্ট
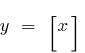 — ব্রেক পয়েন্ট সব পূর্ণসংখ্যা পয়েন্ট
— ব্রেক পয়েন্ট সব পূর্ণসংখ্যা পয়েন্ট
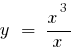 — বিরতি - 0
— বিরতি - 0
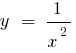 — বিরতি - 0
— বিরতি - 0

 পৃথক অর্জন শেষ সময়ে এই সেগমেন্ট মান বিভিন্ন লক্ষণ, তারপর কিছু সময়ে এই সেগমেন্ট, তিনি একটি মান শূন্য.
পৃথক অর্জন শেষ সময়ে এই সেগমেন্ট মান বিভিন্ন লক্ষণ, তারপর কিছু সময়ে এই সেগমেন্ট, তিনি একটি মান শূন্য.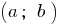 ফাংশন হয়,
ফাংশন হয়, 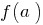 এবং
এবং 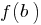 .
. এবং
এবং  যে জন্য সব
যে জন্য সব 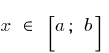 বৈষম্য
বৈষম্য 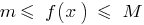 .
.