The continuity of the function at the point
Definition: a Function 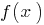 is called continuous at
is called continuous at 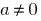 if
if 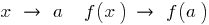 , that is
, that is 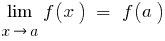 .
.
Continuous functions on the interval
Definition: If a function is 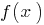 continuous at each point of some interval
continuous at each point of some interval 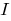 , it is called continuous on the interval
, it is called continuous on the interval 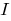 .
.
Continuity properties of functions
- If continuous on wtrysku
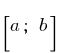 individual acquires at the ends of this segment the values of different signs, then at some point this segment she takes on a value of zero.
individual acquires at the ends of this segment the values of different signs, then at some point this segment she takes on a value of zero. - If on the interval
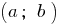 the function is
the function is 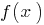 continuous and does not turn into zero on this interval function keeps a constant sign.
continuous and does not turn into zero on this interval function keeps a constant sign. - A function
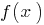 , continuous on an interval
, continuous on an interval 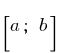 takes on all intermediate values between the values of this function at the extreme points, i.e., between
takes on all intermediate values between the values of this function at the extreme points, i.e., between 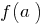 and
and 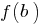 .
. - A function
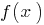 continuous on a segment
continuous on a segment 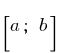 , is restricted on this segment, then there exist two numbers
, is restricted on this segment, then there exist two numbers 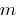 and
and 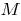 that for all
that for all 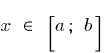 inequality
inequality 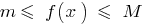 .
. - The amount of the difference and the work is continuous on this interval the function is continuous on the same interval function. The quotient of two continuous functions is a continuous function at all points where the denominator is not peretolchina to zero.
- The inverse of a continuous function on the given interval, is continuous on this interval.
- If the function
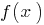 has a derivative at
has a derivative at 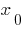 , then it is continuous at that point.
, then it is continuous at that point.
Example of continuity of a function
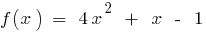 is a continuous function (polynomial)
is a continuous function (polynomial)
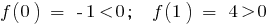 so on the interval (0;1) there is a point
so on the interval (0;1) there is a point 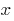 where the function equals 0:
where the function equals 0: 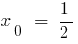
Example of continuity of a function
Example of continuity of a function
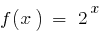 is a continuous function. If
is a continuous function. If
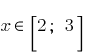 then
then 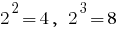 . Because
. Because 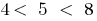 , there is a point
, there is a point 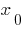 where
where 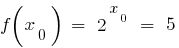 .
.
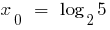
The rule of finding the largest and smallest snakeb functions.
Break point
Definition: Point 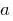 break point function
break point function 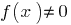 , if the point
, if the point 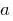 is not the condition that when
is not the condition that when 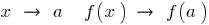 .
.
Examples of functions with break points
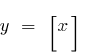 — break points all the integer points
— break points all the integer points
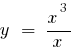 — break - 0
— break - 0
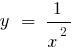 — break - 0
— break - 0

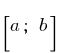 individual acquires at the ends of this segment the values of different signs, then at some point this segment she takes on a value of zero.
individual acquires at the ends of this segment the values of different signs, then at some point this segment she takes on a value of zero.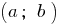 the function is
the function is 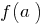 and
and 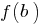 .
.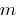 and
and 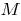 that for all
that for all 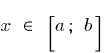 inequality
inequality 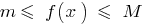 .
.