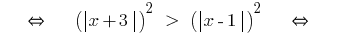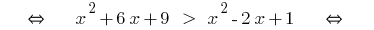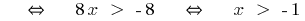Definition: an Inequality with a single variable and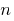 
two expressions with one variable is United with the sign 
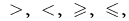which in its General form is written like this: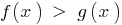 
Definition: a Root (or rozvyazka inequalities) is called the value of a variable that turns an inequality into correct numerical equality.
Razvesti inequality means finding all its roots (interchanges) or to show that they are not.
The area of allowable values of DHS inequality
Definition: the Area of allowable values (range of definition) the bumps — the total scope of functions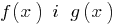 
standing in the left and right parts of the equation.
Find the area of allowable values (odz)
Example
Set the equation: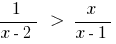 
DHS: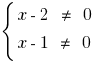 
i.e.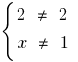 
you can write and so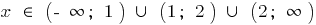 
.
Roughness — implications
When rozwiazan roughness effects are not used (and are used is equivalent to conversion), since it is usually impossible to validate all received rozvytku inequalities-consequences.
Is equivalent to the inequality
Definition: Equivalent to (equivalent to) the bumps two bumps, which for many DHS have the same outcome, that is, every solution of the first inequality is rozvyazka the second, and Vice versa.
Some theorems about equally dominant either equations
Theorem 1: If one of the inequalities to move to another part of the terms with opposite sign, we get nervst equivalent to a given (on any set).
Theorem 2.1: If both sides of an inequality be multiplied or divided by the same positive integer not equal to zero (or to one and the same function that is defined and not equal to zero on the IDS of the given equation), we get the inequality, tantamount given.
Theorem 2.2: If both sides of an inequality be multiplied or divided by the same VMA integer not equal to zero (or to one and the same function, which is defined and WMA on the odz of the given equation), and KRM in order to change the inequality sign to the opposite, we get the inequality, tantamount given.
Theorem 3.1: If both sides 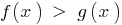take increasing function 
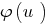(preserving the sign of the inequality) and there is no narrowing of the DHS - specified inequality, the resulting inequality 
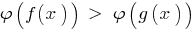to be equivalent to the specified ( DHS).
Theorem 3:2 If both sides 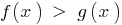take the spotlight function of 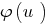changing the sign of inequalities, and there is no narrowing of the DHS - specified inequality, the resulting inequality 
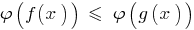to be equivalent to the specified ( DHS).
Corollaries of theorems about equally dominant either inequalities
Consequence: Because the function is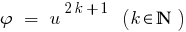 
monotonically increasing,then
.
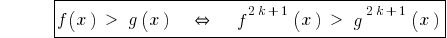In the presentation of both parts to odd natural degree of the resulting inequality, tantamount given.
Consequence: Because the function is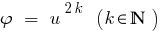 
monotonically increasing only if 
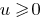,in the case when both sides of an inequality newmn, by lifting both parts of the natural to the even degree get Nernst equivalent to this.
Example 1
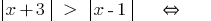(both parts newmn!)
