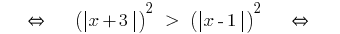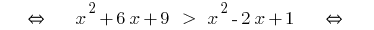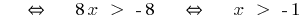Definición: las Desigualdades con una variable de 
dos expresiones con una variable de estados uno con el signo 
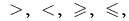que, en términos generales, se escribe así: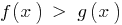 
Definición: la Raíz (o розвязком) de la desigualdad se llama el valor de la variable que convierte la desigualdad en la verdadera igualdad numérica.
Розвязати la desigualdad significa encontrar todas las raíces (aislamiento) o demostrar que no existen.
Margen de tolerancia de la eds de la desigualdad
Definición: el Área de los valores permitidos (área de definición) las irregularidades — el total de área de definición de las funciones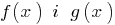 
que están en los lados izquierdo y derecho de la ecuación.
Encontrar el área de los valores permitidos (eds)
Ejemplo
Se establece la ecuación: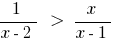 
Eds: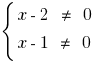 
, es decir,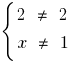 
que se puede grabar y así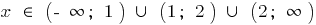 
.
Las desigualdades — las consecuencias de la
Cuando розвязувнні de las irregularidades de las consecuencias de no se utilizan (y se utilizan tienden a convertir), ya que normalmente no puede realizar una comprobación de todos los розвязків de la desigualdad de la investigación.
Constituían la desigualdad
Definición: son Equivalentes (son equivalentes) las irregularidades de dos de las desigualdades, que en multitud de salud tienen la misma salida, es decir, cada decisión de la primera desigualdad es розвязком segunda, y viceversa.
Algunos teoremas sobre равносильности de ecuaciones
Teorema 1: Si de una parte de la desigualdad de transferir a la otra parte de la base de signo contrario, obtendremos нерівнсть, constituyen especificado (cualquier variedad).
El teorema 2.1: Si ambos lados de la parte de la desigualdad se multiplica o divide por un mismo número positivo distinto de cero (o en la misma función que está definida y no es igual a cero en las eds teórico de la ecuación), obtenemos la desigualdad constituyen especificado.
Teorema 2.2: Si ambos lados de la parte de la desigualdad se multiplica o divide por un mismo відємне número distinto de cero (o en la misma función, que se define y відємна en las eds teórico de la ecuación) y, loc, cambiar el signo de la desigualdad en el opuesto, obtenemos la desigualdad, constituyen especificado.
El teorema 3.1: Si de ambos lados de la desigualdad 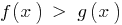tomar la creciente función 
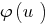(manteniendo el signo de la desigualdad) y si este no se produce un estrechamiento de la eds especificado, la desigualdad, la resultante de la desigualdad 
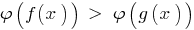es equivalente especificado ( eds).
Teorema 3:2 Si es de ambas partes de la desigualdad 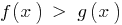de tomar una función 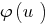, cambiando el signo de la desigualdad, y si este no se produce un estrechamiento de la eds especificado, la desigualdad, la resultante de la desigualdad 
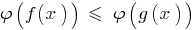es equivalente especificado ( eds).
Las consecuencias de los teoremas de равносильности de las desigualdades
Consecuencia: Dado que la función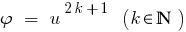 
monótonamente aumenta,
.
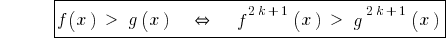Al ofrecer a ambas partes hasta impar natural obtenemos el grado de desigualdad que constituyen este.
Consecuencia: Dado que la función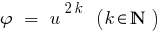 
monótonamente tan sólo aumenta cuando 
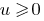,en caso de que ambas partes de la desigualdad невідємні, al levantar ambas partes a un natural de grado obtenemos нерінвість que constituyen este.
Ejemplo 1
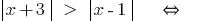(ambos lados de la parte невідємні!)
