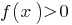Tienden a la conversión de los más simples de las desigualdades
 Si a > 1
Si a > 1
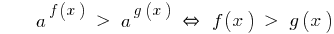
Signo de la desigualdad se mantiene.
Ejemplo 1
Розвяжіть la desigualdad: 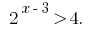
Soluciones:
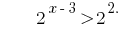
La función 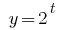 es creciente, por lo tanto приравниваем indicadores
es creciente, por lo tanto приравниваем indicadores
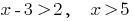
Respuesta: 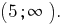
 Si 0 < a < 1
Si 0 < a < 1
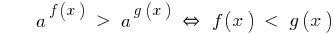
Signo de la desigualdad se invierte.
Ejemplo 2
Розвяжіть la desigualdad: 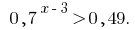
Soluciones:
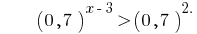
La función de
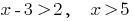
Respuesta: 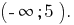
La decisión más complejos de la excelencia de las desigualdades
Con representaron transformaciones
Con representaron una transformación (por el esquema de decisión de la excelencia de las ecuaciones) valor de la desigualdad se reduce a la desigualdad conocido de la especie (cuadrado, fraccionaria o la otra). Después de recibida la decisión de la desigualdad, llegamos a los más simples de excelencia de las desigualdades.
Ejemplo 3
Розвяжіть la desigualdad: 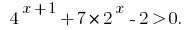
Soluciones:
La sustitución 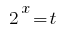 da la desigualdad
da la desigualdad 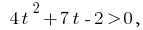
la salida que 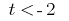 o
o 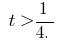
Así 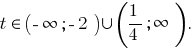
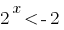 (розвязків no) o
(розвязків no) o 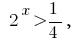 de donde
de donde 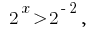 lo hay
lo hay 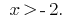
Respuesta: 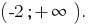
Mediante el método de los intervalos de
Aplicamos en general el método de los intervalos,
- Encontrar eds
- Encontrar los ceros de la función

- Señalar los ceros de la función en la salud y encontrar la marca
 en cada uno de los períodos en que se divide la eds.
en cada uno de los períodos en que se divide la eds. - Escribir la respuesta, teniendo en cuenta el signo de la desigualdad.
Ejemplo 4
Розвяжіть la desigualdad: 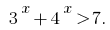
Soluciones:
Permitir que la desigualdad según el método de intervalos. Dada la desigualdad івносильна irregularidades 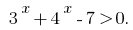
Designaremos 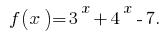
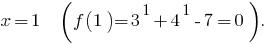
- Eds:
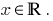
- Los ceros de la función:
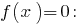
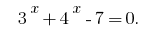
- Dado que la función
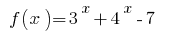 es creciente, entonces el valor de cero, se acepta sólo en un punto, la definición de área:
es creciente, entonces el valor de cero, se acepta sólo en un punto, la definición de área: - Se denota el cero de la función de la eds, encontramos la marca
 en cada uno de los períodos en los que розбвається eds, y registrar la salida de irregularidades
en cada uno de los períodos en los que розбвається eds, y registrar la salida de irregularidades 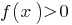
Respuesta: 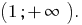
La solución de desigualdades muy similar a los de las ecuaciones, por lo tanto, si Usted no ha encontrado розязання adecuados irregularidades, vaya a la página exponencial de la ecuación.

 Si a > 1
Si a > 1
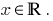
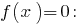
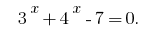
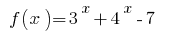 es creciente, entonces el valor de cero, se acepta sólo en un punto, la definición de área:
es creciente, entonces el valor de cero, se acepta sólo en un punto, la definición de área: