Definición: una función Lineal se denomina función de la especie  , donde
, donde 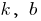 — algunos números
— algunos números
Propiedades de funciones lineales
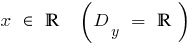
cuando 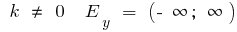
cuando 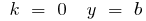
cuando 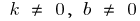 la función ni par ni impar
la función ni par ni impar
si 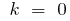 — baño de vapor
— baño de vapor
cuando 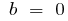 y
y 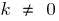 — impar
— impar
al 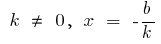 punto de intersección con el eje de
punto de intersección con el eje de 
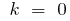 entonces
entonces 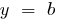 — recta paralela al eje de
— recta paralela al eje de  la
la 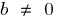 y coincide con el eje de
y coincide con el eje de  la
la 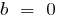
Lineal de la función es continua y диференційовна en toda la recta numérica 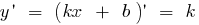
si 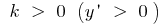 la función crece en toda la recta numérica
la función crece en toda la recta numérica
cuando 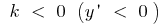 la función decrece en toda la recta numérica
la función decrece en toda la recta numérica
cuando 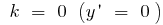 una función se
una función se
- La definición del área

- Valor múltiple

- La paridad, paridad impar
- Los puntos de intersección con los ejes de coordenadas
- La continuidad y дифференцируемость
- El crecimiento y el receso de la
- El calendario de la función lineal-siempre es recta, tangente de un ángulo de inclinación de la recta al eje de la
al
 punto de intersección con el eje de
punto de intersección con el eje de 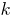
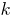 es la pendiente de la recta
es la pendiente de la recta 
si
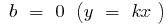 es una recta que pasa por el origen de coordenadas
es una recta que pasa por el origen de coordenadassi
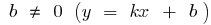 es una recta que no pasa por el origen de coordenadas
es una recta que no pasa por el origen de coordenadas
Gráficos de funciones lineales
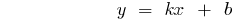
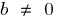
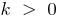
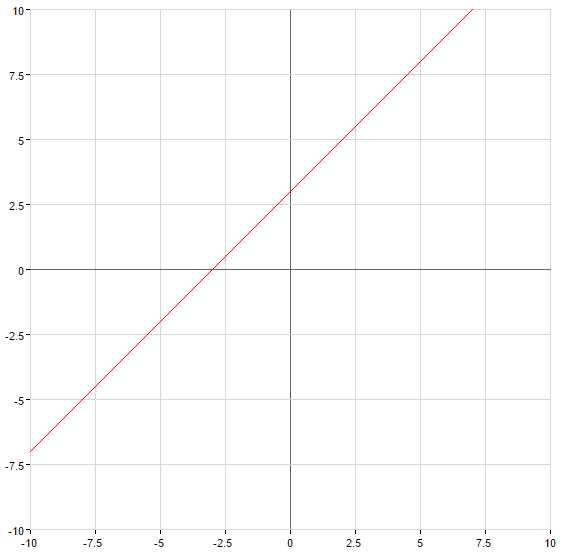
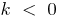
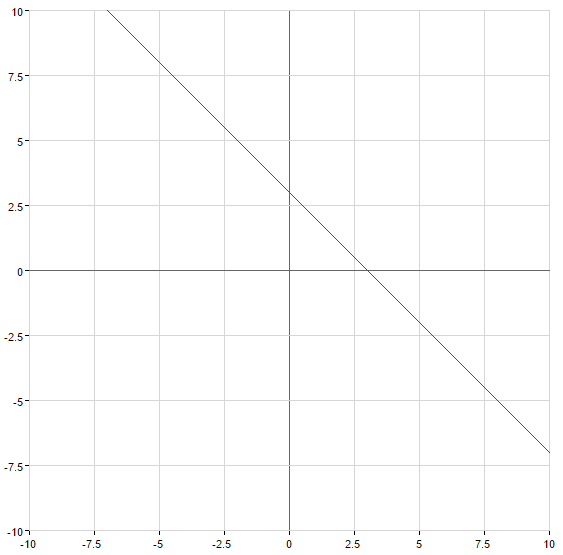
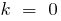
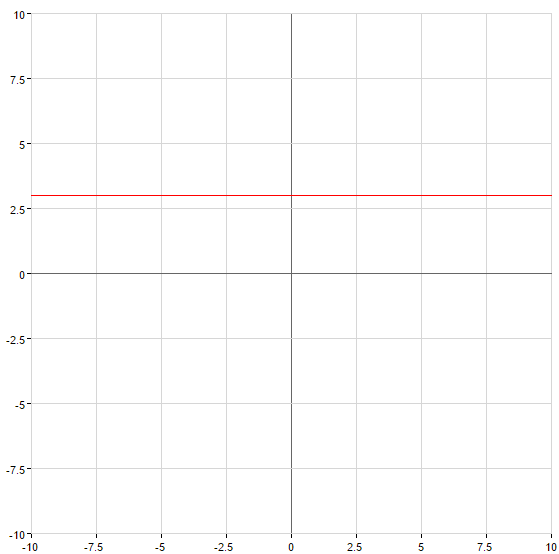
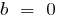
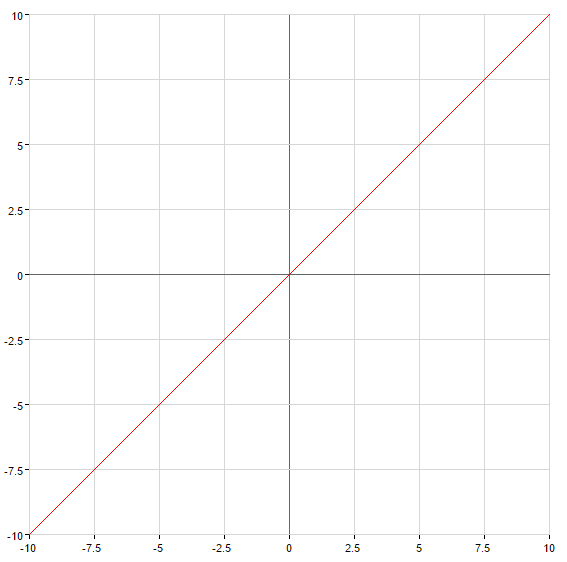



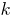
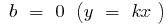 es una recta que pasa por el origen de coordenadas
es una recta que pasa por el origen de coordenadas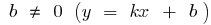 es una recta que no pasa por el origen de coordenadas
es una recta que no pasa por el origen de coordenadas