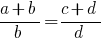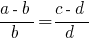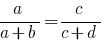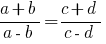Definición: Proporción se llama igualdad de dos relaciones.
o 
.
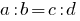La principal propiedad de las proporciones
La obra extremo de los miembros de los miembros de la proporción es igual a la multiplicación de sus medias de los miembros: si
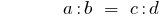entonces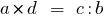 
Propiedades de las proporciones
- La obra extremo de los miembros de los miembros de la proporción es igual a la multiplicación de sus medias de los miembros:
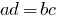. - Cada extremo de un miembro de la relación de aspecto es igual al producto de sus medias de los miembros, dividido por el otro extremo de un miembro.
- En cada relación de aspecto se puede intercambiar o sólo el promedio de los miembros o extremas, o ambos a la vez.
.Ejemplo hallar las proporciones matemáticas
Si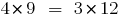 
, lo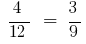 
En la proporción de 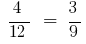cambiar asientos promedio de los miembros o de los extremos de los miembros, entonces recibiremos de nuevo correcta de la igualdad:
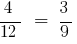y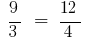 
Los derivados de la relación de aspecto
Si la proporción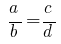 
, lo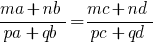 
que se denomina la derivada de la proporción.
El más de uso frecuente derivados de la relación de aspecto
La escala de
Definición: la Escala es la relación de la distancia en el mapa correspondiente a la distancia en la realidad de la zona.
Directamente proporcionales a la magnitud de la
Definición: Dos magnitudes se denominan directamente proporcional, si con el aumento de los valores de una de ellas en varias veces el valor de la otra aumenta en la misma cantidad de veces.
La tarea en directamente proporcionales a la magnitud de la
El lado del cuadrado es igual a 3 дм. Cómo cambia el perímetro de un cuadrado si su lado aumentar 3 veces 4 veces 5 veces?
El lado de un cuadrado de 3 dm de perímetro de 12 dm
El lado de un cuadrado de 9 dm, el perímetro de 36 dm
El lado de un cuadrado de 12 dm, el perímetro de 48 dm
El lado de un cuadrado de 15 dm, el perímetro de 60 dm
Cuando se aumenta el lado de un cuadrado de 3 veces (3 dm, se ha convertido — 9 dm), el perímetro también aumentó en 3 veces (fue de 9 dm, se convirtió en — 36 dm).
De igual modo, al aumentar el lado de un cuadrado en 4 veces (3 dm, se ha convertido — 12 dm), el perímetro también aumentó 4 veces (fue el 12 de dm, se convirtió en — 48 dm).
Conclusión: si aumenta el lado de un cuadrado en varias ocasiones, el perímetro aumenta en la misma cantidad de veces.
El lado del cuadrado es directamente proporcional a su perímetro.
Inversamente proporcionales a la magnitud de la
Definición: Dos magnitudes se denominan обенено proporcionales, si con el aumento de los valores de una de ellas en varias veces el valor de la otra disminuye en la misma cantidad de veces.
La tarea, en el nuevo proporcionales a la magnitud de la
La distancia entre dos pueblos es de 160 km ¿cuánto tiempo se puede llegar de un pueblo a otro, si la velocidad de 10 km/h aumentar 2 veces, 4 veces, 8 veces?
La velocidad, km/h 10 tiempo, h 16
La velocidad, km/h 20 tiempo, h 8
La velocidad, km/h 40 tiempo, h 4
La velocidad, km/h 80 tiempo, h 2
Al aumentar la velocidad en 2 veces (era de 10 km/h, se ha convertido en 20 km/h), el tiempo se redujo (disminuyó) 2 veces (16 h, se ha convertido — 8 horas).
Del mismo modo, cuando el aumento de la velocidad en 4 veces (era de 10 km/h, se convirtió en 40 km/h), el tiempo se redujo (disminuido) en 4 veces (16 h, se ha convertido — 4 h).
Conclusión: cuando aumenta la velocidad en varias veces, el tiempo se reduce en la misma cantidad de veces.
La velocidad es inversamente proporcional al tiempo.
Los números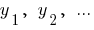 
proporcionales a los números 
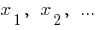, si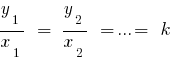 
— coeficiente de proporcionalidad.
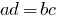