El concepto de la segunda derivada



Que función  tiene derivada
tiene derivada  en todos los puntos de un período determinado. Este derivado, a su vez, es función de
en todos los puntos de un período determinado. Este derivado, a su vez, es función de 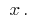 Si la función
Si la función  es diferenciada, su derivada se llama segunda derivada de
es diferenciada, su derivada se llama segunda derivada de  y representan
y representan 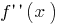 (o
(o 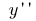 )
)
Ejemplo. 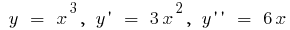
El concepto de convexidad, concavidad y puntos de inflexión de la gráfica функцї
Supongamos que la función  está definida en un intervalo
está definida en un intervalo 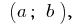 y en el punto que
y en el punto que 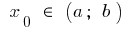 tiene el final de la derivada. Entonces el gráfico de esta función en un punto
tiene el final de la derivada. Entonces el gráfico de esta función en un punto 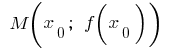 se puede pasar la tangente
se puede pasar la tangente
Si en un barrio de punto de  todos los puntos de la curva de la gráfica de la función
todos los puntos de la curva de la gráfica de la función  (excepto de punto
(excepto de punto 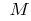 ) se encuentran por encima de la tangente, entonces se dice que la curva (y la función en el punto
) se encuentran por encima de la tangente, entonces se dice que la curva (y la función en el punto  es convexa (o más bien, estrictamente convexa). También, a veces, dicen, que en este caso, la gráfica de la función
es convexa (o más bien, estrictamente convexa). También, a veces, dicen, que en este caso, la gráfica de la función  convertido abultamiento hacia abajo
convertido abultamiento hacia abajo
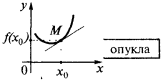
Si en un barrio de punto de  todos los puntos de la curva (excepto de punto
todos los puntos de la curva (excepto de punto 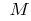 ) están por debajo de la tangente, entonces se dice que la curva (y la función en el punto
) están por debajo de la tangente, entonces se dice que la curva (y la función en el punto  es угнутою (más estrictamente угнутою). También, a veces, dicen, que en este caso, la gráfica de la función convertido abultamiento hacia arriba
es угнутою (más estrictamente угнутою). También, a veces, dicen, que en este caso, la gráfica de la función convertido abultamiento hacia arriba
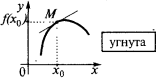
Si el punto  en el eje de abscisas tiene la propiedad de que al pasar de un argumento
en el eje de abscisas tiene la propiedad de que al pasar de un argumento  a través de ella, la curva
a través de ella, la curva  pasa por un lado de la tangente a otra, el punto
pasa por un lado de la tangente a otra, el punto  se llama punto de inflexión de la función de
se llama punto de inflexión de la función de 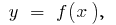 punto de la curva
punto de la curva 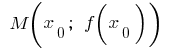 es el punto de inflexión de la gráfica de la función
es el punto de inflexión de la gráfica de la función 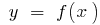
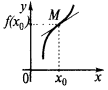
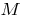 — el punto de inflexión de la gráfica de la función
— el punto de inflexión de la gráfica de la función
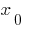 — el punto de inflexión de la función
— el punto de inflexión de la función
En un barrio de punto  : si
: si 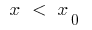 la curva por debajo de la tangente y la
la curva por debajo de la tangente y la 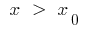 curva por encima de la tangente (o viceversa)
curva por encima de la tangente (o viceversa)
Estudio de la función de bulto, угнутість y el punto de inflexión
Ejemplo. 
La definición del área: 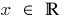
Función continua en cada punto de su dominio
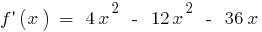
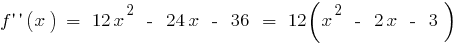
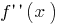 existe en todo el ámbito de la definición de
existe en todo el ámbito de la definición de
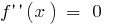 cuando
cuando 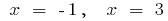
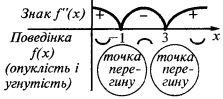
En el intervalo de 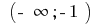 y en el intervalo de
y en el intervalo de 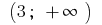 la gráfica de la función
la gráfica de la función  se dirige abultamiento hacia abajo
se dirige abultamiento hacia abajo 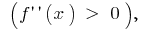 y en el rango de
y en el rango de  la gráfica de la función
la gráfica de la función  dirigido el abultamiento de arriba
dirigido el abultamiento de arriba 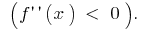
El punto de inflexión: 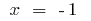 i
i 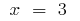 (en estos puntos
(en estos puntos 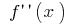 cambia de signo)
cambia de signo)
- Encontrar el área de la definición y los intervalos, en los cuales la función es continua
- Encontrar la segunda derivada de la
- Encontrar internos de un punto de la definición, en los que
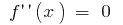 o no existe
o no existe - Señalar recibidos punto en la esfera de la definición, encontrar el signo de la segunda derivada y la naturaleza del comportamiento de la función en cada intervalo, en que se divide el área de la definición de
- Anotar el resultado de la investigación (intervalos de convexidad y concavidad y puntos de inflexión)

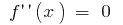 o no existe
o no existe