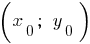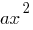Definición: Cuadrática de la función se llama función de la especie 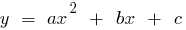 , donde
, donde 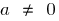
Propiedades de las funciones cuadrática
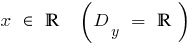
cuando 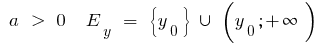
cuando 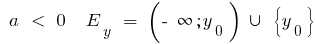
cuando 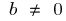 la función ni par ni impar
la función ni par ni impar
si 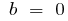 — baño de vapor
— baño de vapor
Cuadrática de la función es continua y диференційовна en toda la recta numérica 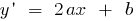
cuando 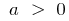 disminuye la
disminuye la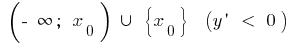 y aumenta
y aumenta 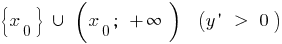 , el
, el 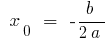 punto mínimo
punto mínimo 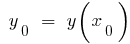 — mínimo
— mínimo
cuando 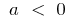 aumenta
aumenta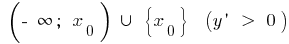 y disminuye en
y disminuye en 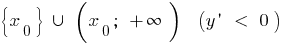 ,
, 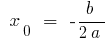 — el punto máximo,
— el punto máximo, 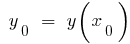 hasta un máximo de
hasta un máximo de
Las coordenadas del vértice de la parábola:
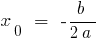 ;
; 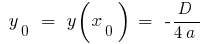 donde
donde 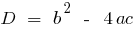
El eje de simetría de la parábola 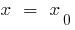
- La definición del área

- Valor múltiple

- La paridad, paridad impar
- La continuidad y дифференцируемость
- El crecimiento y el receso, extremos
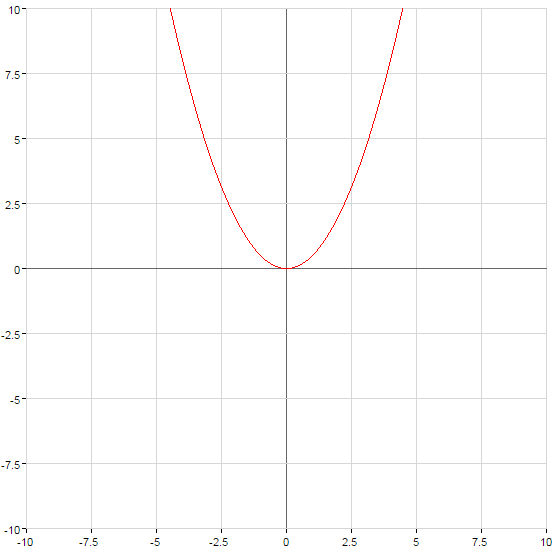
- El calendario cuadrática de la función siempre es una parábola, ramas se dirigen hacia arriba cuando
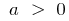 y hacia abajo con
y hacia abajo con 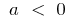
Gráficas de funciones cuadráticas

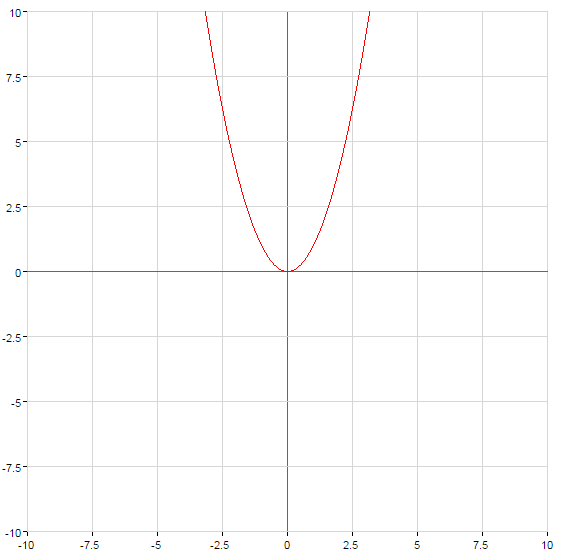

Simetría con respecto al eje 
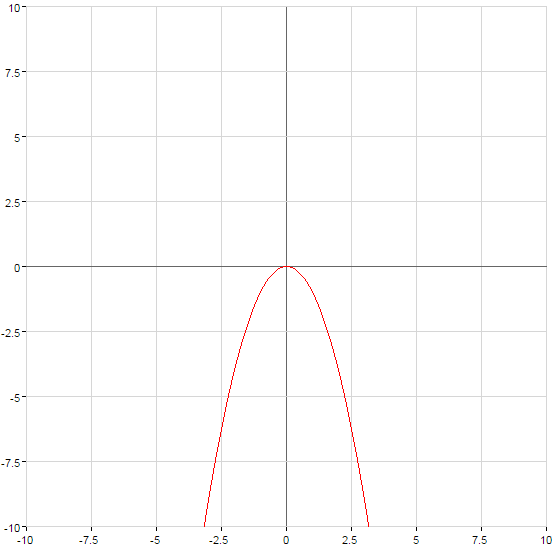

La gráfica de la función cuando se comprime 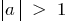 o se estira cuando
o se estira cuando  la cantidad de unidades, que es igual al número y
la cantidad de unidades, que es igual al número y
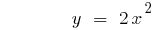
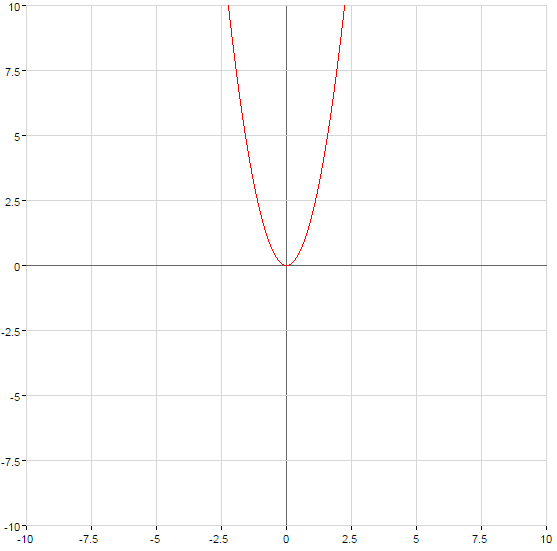
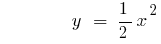
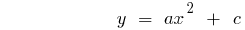
La gráfica de la función se levanta cuando 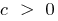 o se baja cuando
o se baja cuando 
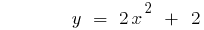
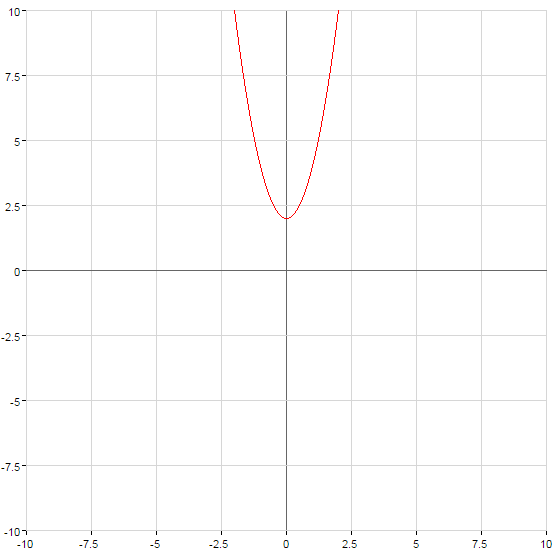
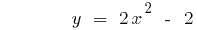
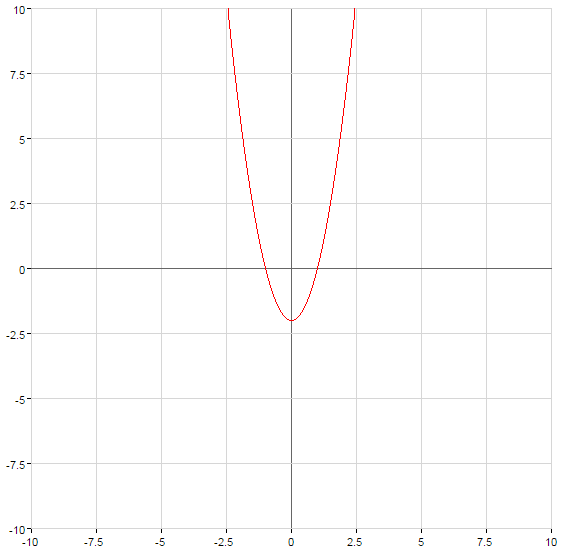
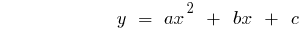
Parábola cruza el eje 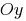 en el punto
en el punto
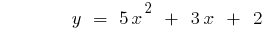
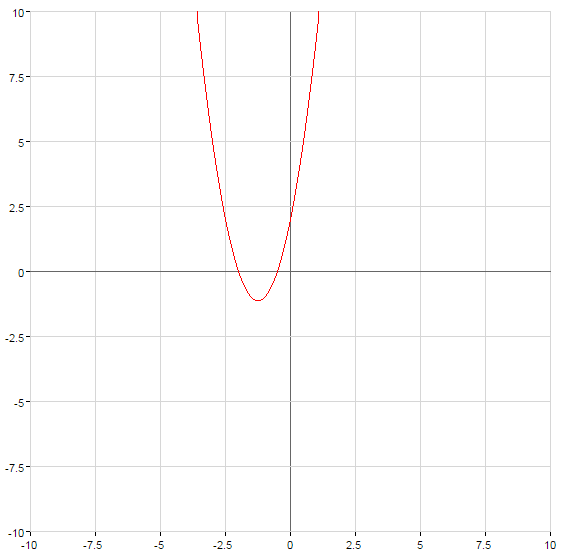
Como construir una curva cuadrática de la función de
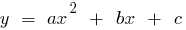
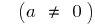
Y la forma de
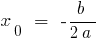
cuando 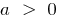 las ramas hacia arriba, con
las ramas hacia arriba, con 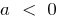 las ramas hacia abajo
las ramas hacia abajo
- Calcular абсцису la cima
- Sustituir
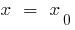 en la ecuación y calcular la ordenada de la cima —
en la ecuación y calcular la ordenada de la cima — 
- Construir un croquis de la parábola (de la especie
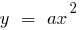 ) con el vértice en el punto de
) con el vértice en el punto de 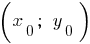
II método
(a lo largo del eje  a
a 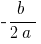 lo largo del eje de la
lo largo del eje de la 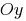 a
a 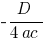 )
)
- Розвязати ecuación cuadrática
- Usando elementales de la transformación de los gráficos, realizar la traslación de la parábola
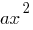




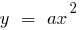 ) con el vértice en el punto de
) con el vértice en el punto de