La monotonía y la constancia de las funciones
Es una condición suficiente ascendente de la función
Si en cada punto del intervalo 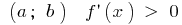 , la función crece en el intervalo
, la función crece en el intervalo
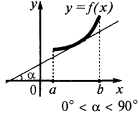
Es una condición suficiente decreciente de la función de
Si en cada punto del intervalo 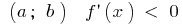 , la función decrece en el intervalo
, la función decrece en el intervalo
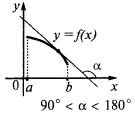
Nota. Estas condiciones son sólo suficientes, pero no son esenciales para el crecimiento y el descendente de la función
Necesaria y suficiente de la condición de la permanencia de la función
La función  es continua en el intervalo
es continua en el intervalo 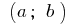 entonces, y sólo entonces, cuando
entonces, y sólo entonces, cuando  en todos los puntos del intervalo completo
en todos los puntos del intervalo completo
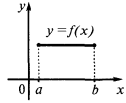
Extremos (máximos y mínimos) de una función
El punto máximo de
Definición: Punto  de la esfera de la definición de la función
de la esfera de la definición de la función  se llama el punto máximo de esta función, si la hay
se llama el punto máximo de esta función, si la hay 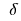 - la vecindad de
- la vecindad de 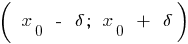 un punto
un punto  , que para todos los
, que para todos los 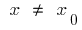 de este barrio se cumple la desigualdad
de este barrio se cumple la desigualdad 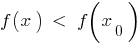
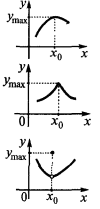
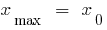 — el punto máximo de
— el punto máximo de
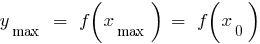 — un máximo de
— un máximo de
El punto mínimo
Definición: Punto  de la esfera de la definición de la función
de la esfera de la definición de la función  se llama el punto mínimo de la función, si hay
se llama el punto mínimo de la función, si hay 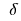 - la vecindad de
- la vecindad de 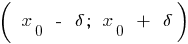 un punto
un punto  , que para todos los
, que para todos los 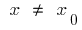 de este barrio se cumple la desigualdad
de este barrio se cumple la desigualdad 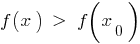
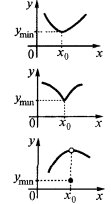
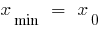 — el punto mínimo
— el punto mínimo
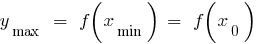 — un mínimo de
— un mínimo de
Los puntos críticos de la
Definición: Internos de los puntos materia de la definición de la función, en los que la derivada de una función es igual a cero o no existe, se llaman críticos
Una condición necesaria de extremo
 — el punto del extremo
— el punto del extremo 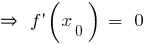 o
o 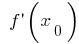 no existe
no existe
(pero no en cada punto  , donde
, donde 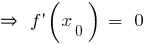 o
o 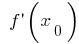 no existe, lo extremo!)
no existe, lo extremo!)
Es una condición suficiente del extremo de la
en el punto de la  señal
señal 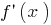 varía con
varía con 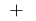 el
el 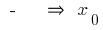 punto máximo de
punto máximo de
en el punto de la  señal
señal 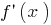 varía con
varía con 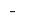 el
el 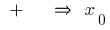 punto mínimo
punto mínimo
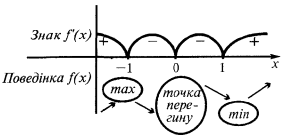
Un ejemplo de la gráfica de la función  , que tiene extremos
, que tiene extremos
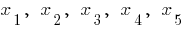 — puntos críticos de
— puntos críticos de
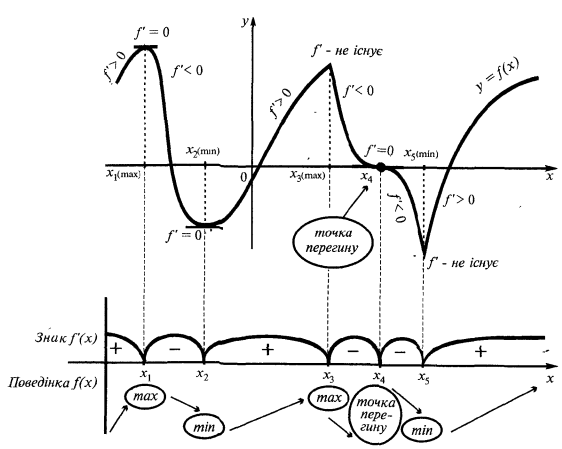
Estudio de la función en la monotonía y extremos
Ejemplo. 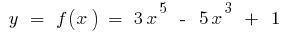
La definición del área: 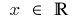
Función continua en cada punto de su dominio
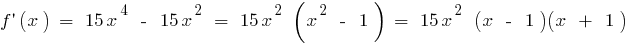
 existe en todo el ámbito de la definición de
existe en todo el ámbito de la definición de
 cuando
cuando 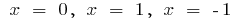
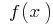 aumenta cuando
aumenta cuando 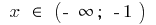 y cuando
y cuando 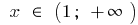
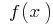 se cae al
se cae al 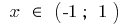
El punto extremo: 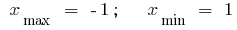
Extremos: 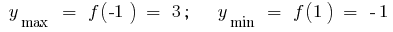
- Encontrar el área de la definición y los intervalos, en los cuales la función es continua
- Encontrar la derivada de la

- Encontrar los puntos críticos, es decir, el interior del punto de la definición, en los que
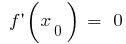 o no existe
o no existe - Indicar los puntos críticos en el ámbito de la definición, encontrar el signo de la derivada y de la naturaleza del comportamiento de la función en cada intervalo, en que se divide el área de la definición de
- Sobre todos y cada uno de los puntos críticos de determinar si es el punto máximo o mínimo o no es el punto del extremo de la
- Grabar потріний el resultado de la investigación (de los intervalos de monotonía y extremos)
El mayor y el menor valor de la función continua en el intervalo
Propiedad: Si la función  es continua en el intervalo y tiene en él un número finito de puntos críticos, ésta adquiere su máximo y el valor mínimo en este tramo, o en los puntos críticos que pertenecen a ese segmento, o en los extremos del segmento
es continua en el intervalo y tiene en él un número finito de puntos críticos, ésta adquiere su máximo y el valor mínimo en este tramo, o en los puntos críticos que pertenecen a ese segmento, o en los extremos del segmento
El hallazgo de mayor y menor valor de función continua en el intervalo
Ejemplo. 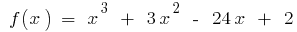 cuando
cuando 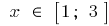
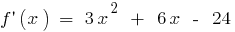
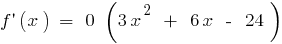 si
si 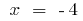 y cuando
y cuando 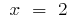
Especificada en la línea 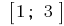 pertenece a un solo punto crítico
pertenece a un solo punto crítico 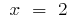
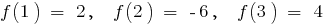

- Encontrar la derivada de la

- Encontrar los puntos críticos (
 o no existe)
o no existe) - Seleccionar los puntos que pertenecen a la especificada en la línea
- Calcular los valores de la función en los puntos críticos y en los extremos del segmento
- Comparar los valores obtenidos y seleccionar uno de ellos, el menor y el mayor

 , que tiene extremos
, que tiene extremos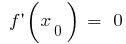 o no existe
o no existe