Monotonie und Dauerhaftigkeit Funktionen
Hinreichende Bedingung Reihenfolge der Funktionen
Wenn in jedem Punkt des Intervalls 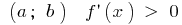 , wird die Funktion steigt in diesem Intervall
, wird die Funktion steigt in diesem Intervall
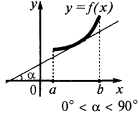
Hinreichende Bedingung abnehmenden Funktionen
Wenn in jedem Punkt des Intervalls 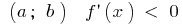 , wird die Funktion nimmt in diesem Intervall
, wird die Funktion nimmt in diesem Intervall
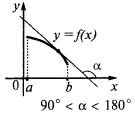
Bemerkung. Diese Bedingungen sind nur ausreichend, sind aber nicht die notwendigen Voraussetzungen für Wachstum und abnehmenden Funktionen
Die notwendige und hinreichende Bedingung der Konstanz der Funktion
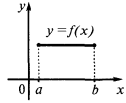
Die Funktion  ist konstant auf dem Intervall
ist konstant auf dem Intervall 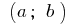 dann und nur dann, wenn
dann und nur dann, wenn  in allen Punkten des ganzen Intervall
in allen Punkten des ganzen Intervall
Extrema (Maxima und minima) der Funktion
Der Punkt des Maximums
Definition: ein Punkt  aus dem Definitionsbereich der Funktion
aus dem Definitionsbereich der Funktion  wird als ein Punkt des Maximums dieser Funktion, wenn es eine
wird als ein Punkt des Maximums dieser Funktion, wenn es eine 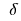 - Umgebung
- Umgebung 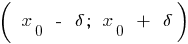 den Punkt
den Punkt  , dass für alle
, dass für alle 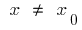 aus dieser Umgebung wird die Ungleichheit
aus dieser Umgebung wird die Ungleichheit 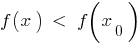
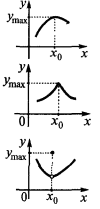
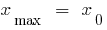 — der Punkt des Maximums
— der Punkt des Maximums
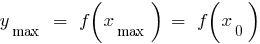 — maximal
— maximal
Der Punkt ein Minimum
Definition: ein Punkt  aus dem Definitionsbereich der Funktion
aus dem Definitionsbereich der Funktion  wird als ein Punkt des Minimums dieser Funktion, wenn es eine
wird als ein Punkt des Minimums dieser Funktion, wenn es eine 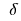 - Umgebung
- Umgebung 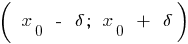 den Punkt
den Punkt  , dass für alle
, dass für alle 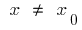 aus dieser Umgebung wird die Ungleichheit
aus dieser Umgebung wird die Ungleichheit 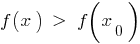
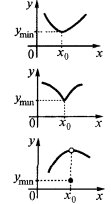
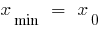 — der Punkt ein Minimum
— der Punkt ein Minimum
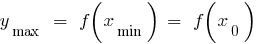 — mindestens
— mindestens
Kritische Punkte
Definition: die Inneren Punkte Definitionsbereich der Funktion, die Ableitung einer Funktion gleich null ist oder nicht vorhanden ist, werden als kritisch
Notwendige Bedingung extre
 — Punkt extre
— Punkt extre 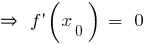 - oder
- oder 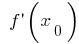 — nicht vorhanden
— nicht vorhanden
(aber nicht in jedem Punkt  , wo
, wo 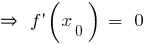 oder
oder 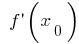 nicht vorhanden ist, wird der extremwert!)
nicht vorhanden ist, wird der extremwert!)
Hinreichende Bedingung extre
in Punkt  Zeichen
Zeichen 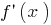 ändert sich mit
ändert sich mit 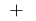 auf
auf 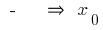 — zu-Punkt-Maximum
— zu-Punkt-Maximum
in Punkt  Zeichen
Zeichen 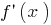 ändert sich mit
ändert sich mit 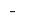 auf
auf 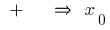 — zu-Punkt-tief
— zu-Punkt-tief
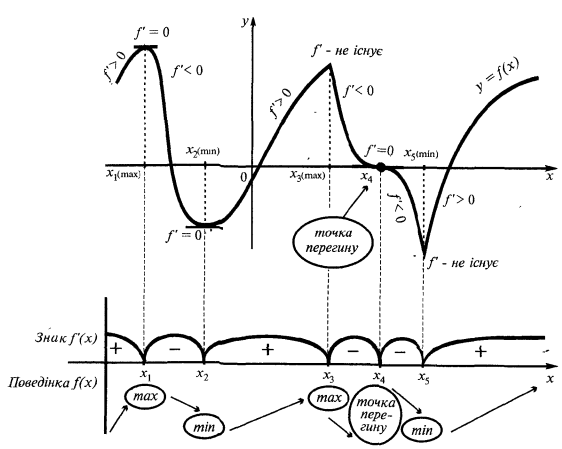
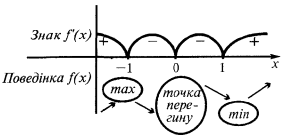
Ein Beispiel für den graph einer Funktion  , Extrema hat
, Extrema hat
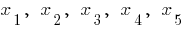 — kritische Punkte
— kritische Punkte
Studieren Sie die Funktionen auf Monotonie und Extrema
Beispiel. 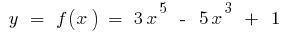
Bereich "Definition": 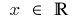
Funktion Continuous in jedem Punkt Ihres Gebietes bestimmen
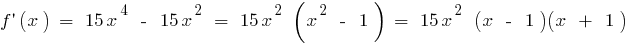
 es gibt auf dem gesamten Definitionsbereich
es gibt auf dem gesamten Definitionsbereich
 bei
bei 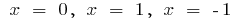
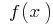 steigt bei
steigt bei 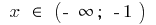 und bei
und bei 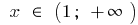
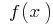 nachlässt bei
nachlässt bei 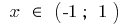
Punkte extre: 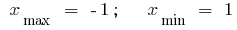
Extrema: 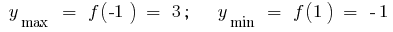
- Suchen Sie den Bereich bestimmen und die Intervalle, auf denen die Funktion kontinuierlich ist
- Eine abgeleitete

- Eine kritische Punkte, d.h. die inneren Punkte der Bereiche bestimmen, in denen
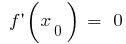 oder nicht vorhanden ist
oder nicht vorhanden ist - Bezeichnen kritische Punkte auf Definitionsbereich, eine abgeleitete Zeichen und das Verhalten der Funktion auf jedem Intervall, auf die sich ein Bereich definieren
- Relativ zu jedem kritischen Punkt bestimmen, ob es ein Punkt des Maximums oder Minimums oder nicht ist ein Punkt, der extre
- Notieren потріний das Ergebnis der Studie (die Intervalle der Monotonie und Extrema)
Größten und kleinsten Wert der Funktion, kontinuierliche auf der Strecke
Eigenschaft: Wenn die Funktion  kontinuierlich auf der Strecke und hat darauf eine endliche Anzahl von kritischen Punkten, dann erwirbt Sie Ihren größten und kleinsten Werte auf dieser Strecke entweder in kritischen Punkten, die Zugehörigkeit zu diesem Segment, oder auf die Endpunkte des Intervalls
kontinuierlich auf der Strecke und hat darauf eine endliche Anzahl von kritischen Punkten, dann erwirbt Sie Ihren größten und kleinsten Werte auf dieser Strecke entweder in kritischen Punkten, die Zugehörigkeit zu diesem Segment, oder auf die Endpunkte des Intervalls
Finden größten und kleinsten Wert der Funktion, kontinuierliche auf der Strecke
Beispiel. 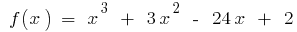 bei
bei 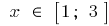
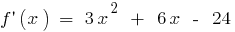
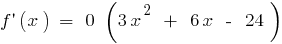 bei
bei 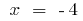 und bei
und bei 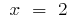
Bestimmten Segment 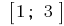 gehört nur der kritische Punkt
gehört nur der kritische Punkt 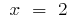
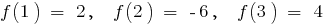

- Eine abgeleitete

- Eine kritische Punkte (
 oder nicht vorhanden)
oder nicht vorhanden) - Wählen Sie kritische Punkte, die dem angegebenen Schnitt
- Berechnen Sie die Funktionswerte an den kritischen Punkten und an den enden geschnittener
- Vergleichen Sie die erhaltenen Werte und wählen Sie aus Ihnen die kleinste und die größte

 , Extrema hat
, Extrema hat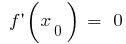 oder nicht vorhanden ist
oder nicht vorhanden ist