Definition: Lassen Sie die Funktion 
definiert auf der ganzen Zahlengeraden. Die Zahl 
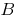heißt Grenzwert der Funktion bei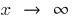 
, wenn für jeden 
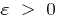gibt es eine solche Zahl 
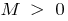, dass für alle 
, die Bedingung zu 
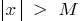, wird die Ungleichheit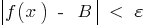 
Wenn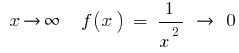 
, dann gibt es bei den großen (modulo) Werten die Anzahl der 
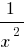sehr wenig Verschieden von der Zahl 0
Wenn das Verhalten der Funktion variiert bei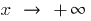 
und wenn 
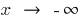, dann separat zu betrachten 
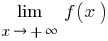(in der Definition nehmen 
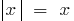) und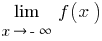 
(in der Definition nehmen 
)
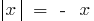Die Grenze der Sequenz
Da die Sequenz ist eine Funktion der natürlichen argument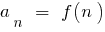 
, das die Bestimmung der Grenze der Reihenfolge bei der 
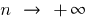vollkommen übereinstimmt mit der Definition der Grenzwert der Funktion bei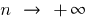
Definition: eine Zahl 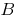heißt Grenzwert einer Sequenz 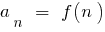, wenn für jeden 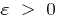gibt es eine solche Zahl 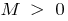, dass für alle 
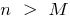, wird die Ungleichheit 
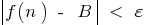dh
Wenn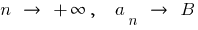 
, dann
Vergleich von exponentiellen Wachstum, exponentiellen und logarithmischen Funktionen
- Bei
,
das heißt
Wenn 
, dann bei der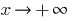 
Funktion 
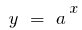wächst schneller als jede exponentiellen Funktion 
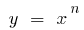, wo 
eine Natürliche Zahl
Grafisch ist diese Aussage bedeutet, dass bei ausreichend großen Werten wird der graph der Funktion 
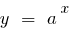(wo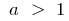 
) befindet sich über dem Diagramm Funktion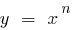 
- Bei
,
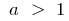
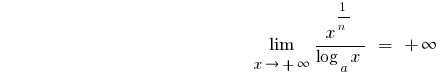das heißt
,
Bei großen ;
,
deshalb
Wenn die Funktion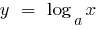 
steigt langsamer als die Funktion 
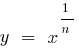(und vor allem langsamer als die Funktion 
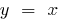oder Funktion 
)
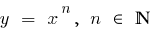Grafisch ist diese Aussage bedeutet, dass bei ausreichend großen Werten wird der graph der Funktion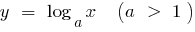 
befindet sich unter dem Graphen der Funktion 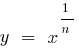(und noch mehr unter Funktionsgraphen )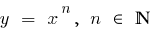