Definition: Асимптота Kurve ist eine gerade, die unbeschränkt nähert sich die Kurve bei der Entfernung von ii in нескінечність.
Vertikale Asymptoten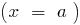 
— vertikale асимптота, 
bei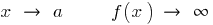 
Vertikale асимптота kann an dem Punkt 
, wenn der Punkt schränkt die offenen Zwischenräume Definitionsbereich dieser Funktionen und die Punkte die Funktion gegen unendlich strebt.
Beispiele für vertikale асимптот
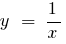
Bei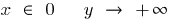 
Bei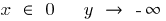 
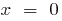— vertikale асимптота
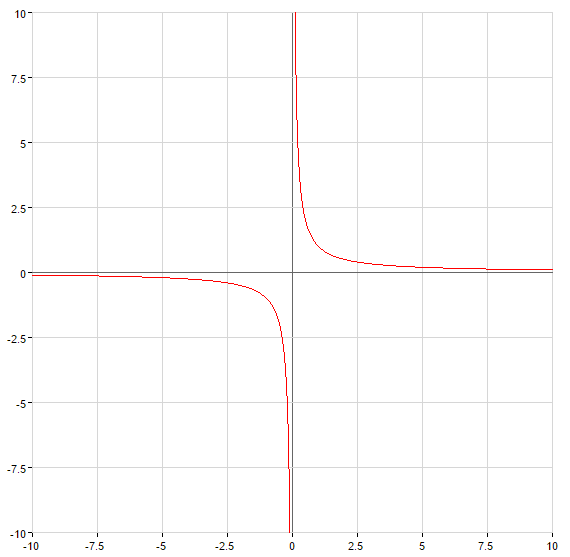
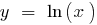
Bei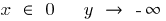
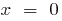— vertikale асимптота
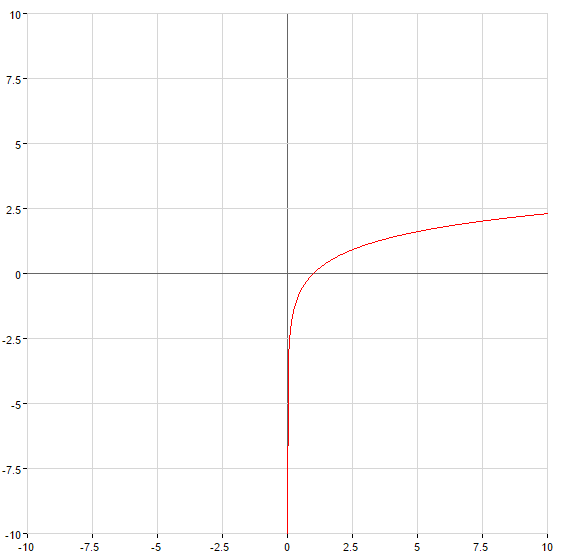
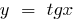
Bei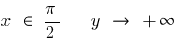 
Bei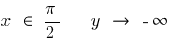 
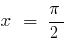— vertikale асимптота
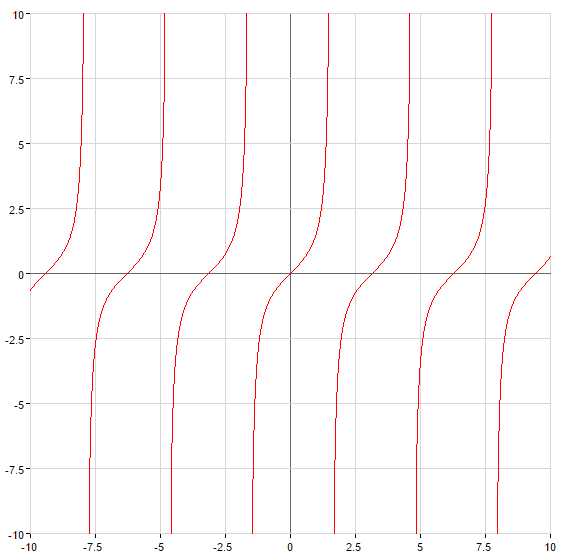
Schräge und horizontale Asymptoten 
- Wenn
— gebrochene-rationale Funktion, deren Grad der Zähler um eins größer ist als der Grad im Nenner, das ganze Bauteil markieren und verwenden die Bestimmung der Asymptoten. - Im Allgemeinen Fall der Gleichung der schrägen und horizontalen асимптот erhalten werden unter Verwendung von Formeln
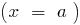
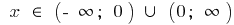
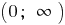
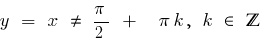
— gebrochene-rationale Funktion, deren Grad der Zähler um eins größer ist als der Grad im Nenner, das ganze Bauteil markieren und verwenden die Bestimmung der Asymptoten.