Die zunehmende Funktion
Definition: eine Funktion  heißt mit steigendem in einiger Menge
heißt mit steigendem in einiger Menge 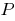 , wenn Sie einen größeren Wert des Arguments aus dieser Reihe entspricht dem größeren Wert der Funktion.
, wenn Sie einen größeren Wert des Arguments aus dieser Reihe entspricht dem größeren Wert der Funktion.
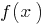 — steigt, wenn für alle
— steigt, wenn für alle 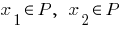
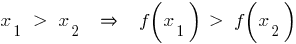
Eigenschaften mit steigendem Funktionen
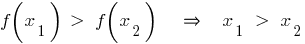
 — zunehmende Funktion
— zunehmende Funktion
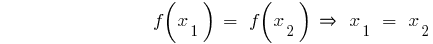 — zunehmende Funktion
— zunehmende Funktion
- Wenn die Funktion
 steigt in einiger Menge
steigt in einiger Menge 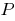 , dann einen größeren Wert der Funktion entspricht dem höheren Wert des Arguments aus dieser Reihe
, dann einen größeren Wert der Funktion entspricht dem höheren Wert des Arguments aus dieser Reihe - Die Summe mehrerer steigenden auf dieser Menge von Funktionen ist eine wachsende Funktion auf dieser Menge.
- Wenn die Funktion
 steigt, dann ist die zu Ihr inverse Funktion ebenfalls erhöht.
steigt, dann ist die zu Ihr inverse Funktion ebenfalls erhöht. - Wenn bei der Erstellung der Funktion
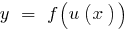 Funktion
Funktion 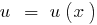 Funktion steigt
Funktion steigt 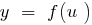 steigt, dann ist die Funktion
steigt, dann ist die Funktion 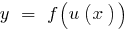 steigt. Das Ergebnis der konsequenten Anwendung von zwei steigenden Funktionen - Erhöhung Funktion.
steigt. Das Ergebnis der konsequenten Anwendung von zwei steigenden Funktionen - Erhöhung Funktion. - Das Ergebnis der konsequenten Anwendung der zunehmenden und abnehmenden Funktionen eine Funktion ist im schwinden Begriffen.
- Jedes wachsende auf einer gegebenen Menge jede Funktion gewinnt Ihre Bedeutung nur in einem Punkt aus dieser Reihe.
Ein Zeichen der zunehmenden Funktionen
Wenn 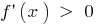 in jedem Punkt des Intervalls
in jedem Punkt des Intervalls  , wird die Funktion
, wird die Funktion  steigt in diesem Intervall.
steigt in diesem Intervall.
Beispiele für Funktionen wachsen auf dem gesamten Definitionsbereich
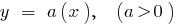
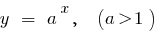
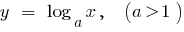
Die absteigende Funktion
Definition: die Funktion  heißt abnehmenden auf einigen Set
heißt abnehmenden auf einigen Set 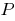 , wenn Sie einen größeren Wert des Arguments aus dieser Reihe entspricht dem größeren Wert der Funktion.
, wenn Sie einen größeren Wert des Arguments aus dieser Reihe entspricht dem größeren Wert der Funktion.
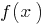 — kommt, wenn für alle
— kommt, wenn für alle 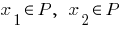
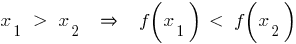
Eigenschaften des abnehmenden Funktionen
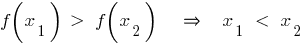
 — abnehm-Funktion
— abnehm-Funktion
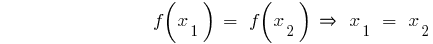 — abnehm-Funktion
— abnehm-Funktion
- Wenn die Funktion
 спадаєна einigen Set
спадаєна einigen Set 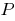 , das einen größeren Wert der Funktion entspricht dem kleineren Wert des Arguments aus dieser Reihe
, das einen größeren Wert der Funktion entspricht dem kleineren Wert des Arguments aus dieser Reihe - Die Summe mehrerer absteigenden auf dieser Menge von Funktionen ist eine abnehmende Funktion auf dieser Menge.
- Wenn die Funktion
 nachläßt, dann ist die zu Ihr inverse Funktion auch nachläßt.
nachläßt, dann ist die zu Ihr inverse Funktion auch nachläßt. - Wenn bei der Erstellung der Funktionen
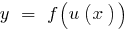 Funktion
Funktion 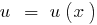 nachläßt und die Funktion
nachläßt und die Funktion 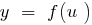 nachläßt, wird die Funktion
nachläßt, wird die Funktion 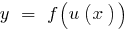 nachläßt. Das Ergebnis der konsequenten Anwendung der beiden abnehm-Funktionen - zunehmende Funktion.
nachläßt. Das Ergebnis der konsequenten Anwendung der beiden abnehm-Funktionen - zunehmende Funktion. - Das Ergebnis der konsequenten Anwendung der zunehmenden und abnehmenden Funktionen eine Funktion ist im schwinden Begriffen.
- Jede absteigende auf einer gegebenen Menge jede Funktion gewinnt Ihre Bedeutung nur in einem Punkt aus dieser Reihe.
Ein Zeichen der abnehmenden Funktion
Wenn 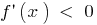 in jedem Punkt des Intervalls
in jedem Punkt des Intervalls  , wird die Funktion
, wird die Funktion  nimmt in diesem Intervall.
nimmt in diesem Intervall.
Beispiele für Funktionen, спадающими auf dem gesamten Definitionsbereich
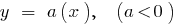
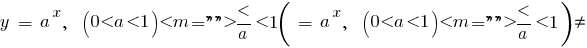
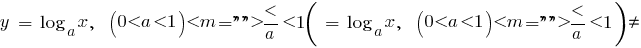

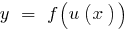 Funktion
Funktion 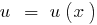 Funktion steigt
Funktion steigt 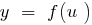 steigt, dann ist die Funktion
steigt, dann ist die Funktion