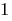Definition: Logarithmische Gleichung — Gleichung, in der Variable steht unter dem Zeichen der Logarithmus..
Um gut in der Lage, розвязувати logarithmische Gleichungen, muss man in der Lage sein, den Verhältnissen des Logarithmus.
Gleichwertiges Umwandlung der einfachsten logarithmischen Gleichungen.
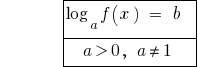
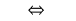
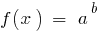
Da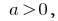 
ist 
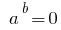und deshalb DHS entry-Gleichung automatisch berücksichtigt.
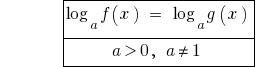
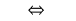
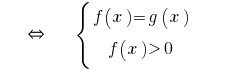oder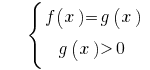 
Auch die Lösung der einfachsten logarithmischen Gleichungen
Beispiel 1
Розвяжіть Gleichungen: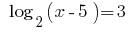 
Lösung:
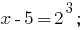
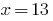
Antwort: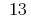 
Beispiel 2
Розвяжіть Gleichungen: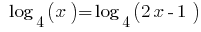 
Lösung:
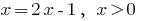(DHS auch berücksichtigt)
Dann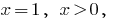 
also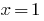 
Antwort: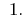 
Schema der Lösung komplexer logarithmische Gleichungen
- Die Verwendung von Gleichungen-Folgen
- Verwendung der Eigenschaften der entsprechenden Funktionen
- Verwendung gleichwertige Transformationen
Wie розвязати Gleichung logarithmisch
Mit Hilfe der Formeln логарифмирования und Potenzierung Gleichung reduzieren, die an den einfachsten (dabei berücksichtigen DHS Primar-und achten darauf, dass die Wurzeln nicht zu verlieren, wenn звужуванні DHS). Nach der Transformation, wenn Sie nicht möglichst einfachen normalen Gleichungen eingeben versuchen Ersatz der Variablen.
Beispiele für die Lösung von logarithmischen Gleichungen
Beispiel 3 (verwenden von Formeln логарифмирования)
Розвяжіть Gleichungen: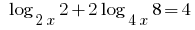 
Lösung:
Indem Sie an der Basis 2, so erhalten wir Gleichung gleichwertiges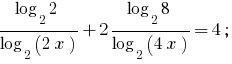 
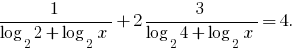
Ersatz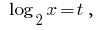 
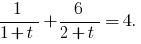
Dann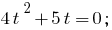 
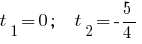
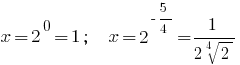
Antwort: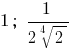 
Beispiel 4 (Verwendung der Eigenschaften logarithmische Funktionen)
Розвяжіть Gleichungen: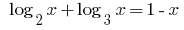 
Lösung:
Die Funktion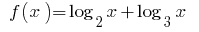 
steigt auf den Bereich der Definition 
als Summe von zwei steigenden Funktionen, und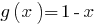 
kommt. Daher ist die angegebene Gleichung hat eine einzige Wurzel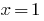
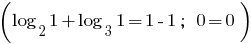
Antwort: 