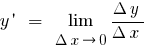
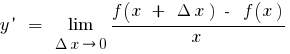
Definition:die Ableitung der Funktion 
im Punkt 
heißt Grenzwert des Verhältnisses des Zuwachses einer Funktion in einem Punkt zum Zuwachs des Arguments, als die Schrittweite des Arguments auf null (entspricht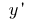 
oder 
)
Der Vorgang der Feststellung der abgeleiteten heißt Unterscheidung
Der Begriff des Wachstums argument und Funktion
Der Zuwachs des Arguments
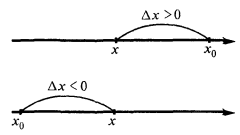
Inkrement-Funktion
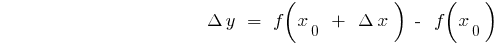
Die Ableitungen der elementaren Funktionen
Die Ableitungen der elementaren Funktionen sind mit Hilfe der Tabelle:
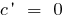
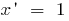
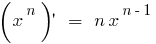
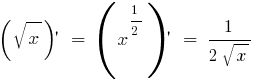
Alle Ableitungen der elementaren Funktionen finden Sie hier!
Besteht die Funktion. Wie eine strukturierte Funktion
Ableitung einer Summe (Differenz) zweier Funktionen, die jeweils eine abgeleitete, gleich der Summe (Differenz) der Ableitungen dieser Funktionen:
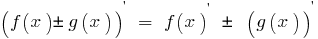
Abgeleitete Werke von zwei Funktionen, die jeweils die abgeleitete ist gleich der Summe der Werke von einzelnen Funktionen auf der Ableitung der zweiten Funktion:
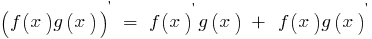
Abgeleitete Anteile Aktien der beiden Funktionen f(x) und g(x), die jeweils eine Ableitung und g(x)≠0, finden sich nach der Formel
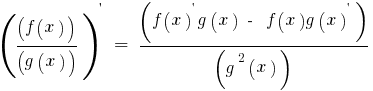
Konstanten Faktor kann man für die Zeichen-Derivat:
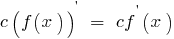
Die Formel nennen die Regeln differenzieren.
Geometrische Bedeutung der Ableitung
Tangente an die Kurve in einem gegebenen Punkt 
wird als Grenzwert für die Bestimmung der Sekante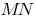 
, wenn sich der Punkt 
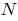nähert sich entlang der Kurve zu einem Punkt
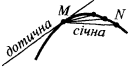
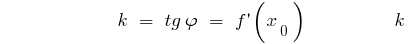— Steigung der Tangente
Die Gleichung der Tangente an den Graphen der Funktion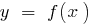 
im Punkt mit абцисою 
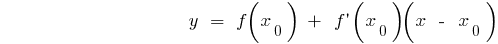
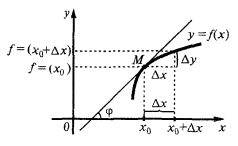
Der Wert der Ableitung an der Stelle gleich ein Ecken-Verhältnis für die Tangente an den Graphen einer Funktion in einem Punkt mit абцисою und gleich тангенсу Winkel dieser Tangente zur Achse 
Die physikalische Bedeutung der Ableitung
Ableitung charakterisiert die Geschwindigkeit der änderung der Funktion bei änderung des Arguments
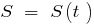— die Abhängigkeit des zurückgelegten Weges von der Zeit
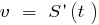— die Geschwindigkeit der geradlinigen Bewegung
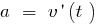— Beschleunigung der geradlinigen Bewegung