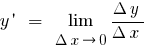
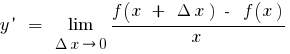
Определение: Производной функции 
в точке 
называется предел отношения приращения функции в точке к приращению аргумента, когда приращение аргумента стремится к нулю (можно обозначить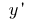 
или 
)
Операция нахождения производной называется дифференцированием
Понятие прироста аргумента и функции
Прирост аргумента
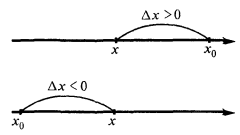
Приращение функции
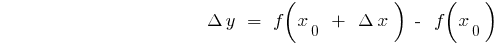
Производные элементарных функций
Производные элементарных функций находятся с помощью таблицы:
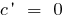
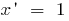
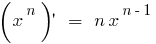
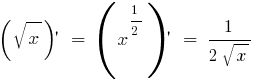
Составлена функция. Как найти составленную функцию
Производная суммы (разности) двух функций, каждая из которых имеет производную, равна сумме (разности) производных этих функций:
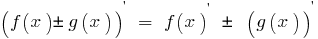
Производная произведения двух функций, каждая из которых имеет производную, равна сумме произведений каждой функции на производную второй функции:
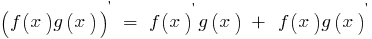
Производную доли доли двух функций f(x) и g(x), каждая из которых имеет производную и g(x)≠0, находят по формуле
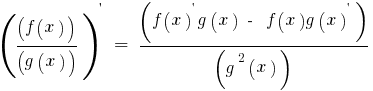
Постоянный множитель можно выносить за знак производной:
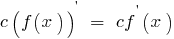
Приведенные формулы называют правилами дифференцирования.
Геометрический смысл производной
Касательной к кривой в данной точке 
называется предельное положение секущей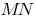 
, когда точка 
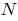приближается вдоль кривой к точке
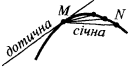
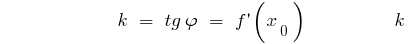— угловой коэффициент касательной
Уравнение касательной к графику функции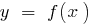 
в точке с абцисою 
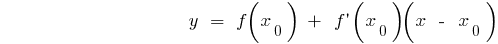
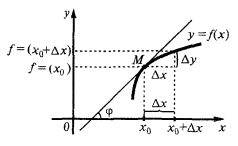
Значение производной в точке равно угловому коэффициенту касательной к графику функции в точке с абцисою и равен тангенсу угла наклона этой касательной к оси 
Физический смысл производной
Производная характеризует скорость изменения функции при изменении аргумента
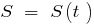— зависимость пройденного пути от времени
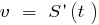— скорость прямолинейного движения
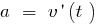— ускорение прямолинейного движения