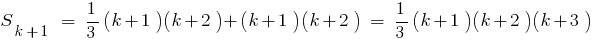Определение: Последовательность —переменная величина, зависит от натурального числа (то есть функция натурального аргумента).
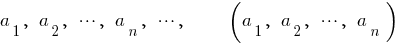 — члены (элементы) последовательности
— члены (элементы) последовательности
Если элементы — действительные числа, то последовательность называется числовой
Примеры
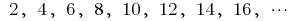 — последовательность четных натуральных чисел
— последовательность четных натуральных чисел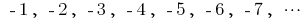 — последовательность целых отрицательных чисел
— последовательность целых отрицательных чисел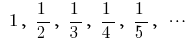 — последовательность чисел, обратных к натуральным
— последовательность чисел, обратных к натуральным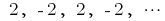 — числовая последовательность
— числовая последовательность
Возрастающие и убывающие последовательности
Определение: Последовательность называется возрастающей, если каждый ее последующий член больше предыдущего: 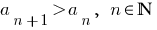 (первая последовательность в примерах).
(первая последовательность в примерах).
Определение: Последовательность называется убывающей, если 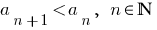 (вторая и третья последовательности в примерах).
(вторая и третья последовательности в примерах).
Метод математической индукции
Используеться для доказательства утверждений 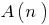 о числовые последовательности или о выражениях, зависящих от натурального числа, в формулировку которых явно или неявно присутствуют слова "для любого натурального
о числовые последовательности или о выражениях, зависящих от натурального числа, в формулировку которых явно или неявно присутствуют слова "для любого натурального  "
"
Схема доказательства утверждений с помощью метода математической индукции
- Проверяем, выполняется ли данное утверждение при
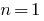 (иногда начинают с
(иногда начинают с 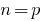 )
) - Предполагаем, что заданное утверждение справедливо при
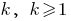 (второй вариант — при
(второй вариант — при 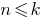 )
) - Доводим (опираясь на предположение) справедливость нашего утверждения и при
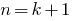
- Делаем вывод, что данное утверждение справедливо для любого натурального числа
 (для любого
(для любого 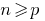 )
)
Пример.
Доказать: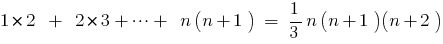
Розвязання. Для удобства записи обозначим 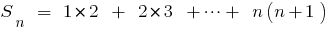
- При
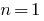 выполняется равенство
выполняется равенство 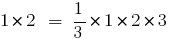
- Предполагаем, что заданная равенство правильная при
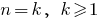 , то есть
, то есть 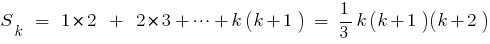
- Докажем, что равенство выполняется и при
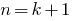 , то есть докажем, что
, то есть докажем, что 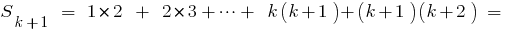
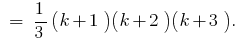 Учитывая, что
Учитывая, что 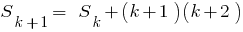 , получаем
, получаем 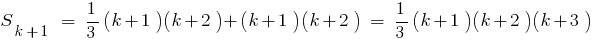
- Следовательно, заданная равенство правильная для любого натурального


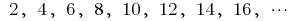 — последовательность четных натуральных чисел
— последовательность четных натуральных чисел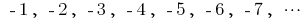 — последовательность целых отрицательных чисел
— последовательность целых отрицательных чисел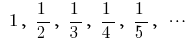 — последовательность чисел, обратных к натуральным
— последовательность чисел, обратных к натуральным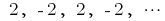 — числовая последовательность
— числовая последовательность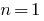 (иногда начинают с
(иногда начинают с 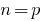 )
)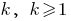 (второй вариант — при
(второй вариант — при 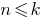 )
)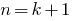
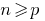 )
)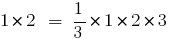
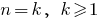 , то есть
, то есть 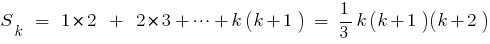
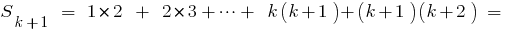
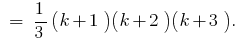 Учитывая, что
Учитывая, что 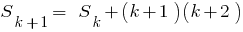 , получаем
, получаем