Иррациональные уравнения

Понятие иррационального уравнения

Определение: Иррациональное уравнение — уравнение, содержащее переменную под знаком корня -ой степени.

Решению иррациональных уравнений

1. С помощью подъема обеих частей иррационального уравнения к одной степени

При поднесении обеих частей уравнения к степени нечетного (1,3,5,7....) получаем уравнение, равносильное заданному (на его ОДЗ)

Пример 1:

Розвяжіть уравнения: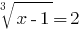

Решения: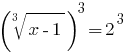





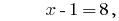
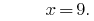
Ответ: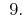

При поднесении обеих частей уравнения в парного степеня (2,4,6,8....) могут появиться посторонние корни, которые отсеют проверкой.

Пример 2:

Розвяжіть уравнения: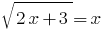

Решения: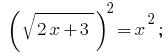



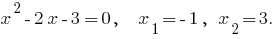
Проверка: При 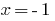имеем 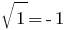- неверное равенство, следовательно, 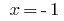- посторонний корень.

При 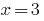имеем 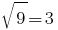- верное равенство, следовательно, 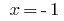- корень заданного уравнения.

Ответ: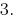

2. С помощью замены переменных

Если в уравнение переменная входит в одном и том же виде, то зучно соответствующее выражение с переменной обозначить одной буквой (новой переменной).

Пример 3:

Розвяжіть уравнения: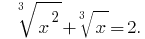

Решение: Обозначим 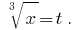Тогда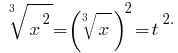

Получаем уравнение: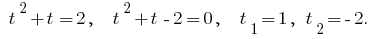

Выполняем обратную замену: 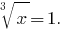Тогда или 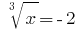отсюда .

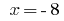При 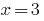имеем 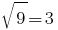- верное равенство, следовательно, 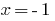- корень заданного уравнения.

Ответ: