Определение: Многочленом от одной переменной  — это многочлен вида
— это многочлен вида 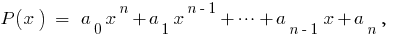 где
где 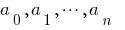 — числовые коэффициенты.
— числовые коэффициенты.
Определение: Если 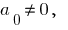 то этот многочлен называется многочленом
то этот многочлен называется многочленом  -ой степени относительно переменной
-ой степени относительно переменной  .
.
Член 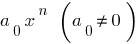 называется старшим членом многочлена
называется старшим членом многочлена 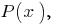 a
a 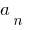 — его свободным членом.
— его свободным членом.
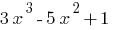 — многочлен третьей степени.
— многочлен третьей степени.
Тождественно равные многочлены от одной переменной
Определение: Два многочлена называются тождественно равными, если они принимают равные значения при всех значениях переменной.
Свойства тождественного равенства многочленов от одной переменной
- Если многочлен
 тождественно равен нулю (то есть приобретает нулевых значений при всех значениях
тождественно равен нулю (то есть приобретает нулевых значений при всех значениях  ), то все его коэффициенты равны нулю.
), то все его коэффициенты равны нулю. - Если два многочлена
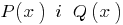 тождественно равны (то есть приобретают одинаковые значения при всех значениях
тождественно равны (то есть приобретают одинаковые значения при всех значениях  ), то они совпадают (то есть их степени равны и коэффициенты при одинаковых степенях равны).
), то они совпадают (то есть их степени равны и коэффициенты при одинаковых степенях равны).
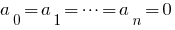
Деление многочлена на многочлен
Определение: Если для двух многочленов 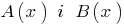 можно найти такой многочлен
можно найти такой многочлен 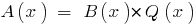 , то говорят, что
, то говорят, что 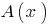 делится на
делится на  .
.
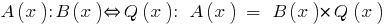
Пример
Поскольку, 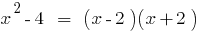 , то многочлен
, то многочлен 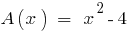 делится на многочлен
делится на многочлен 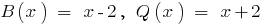
Деление многочлена на многочлен з остачею
Определение: Многочлен 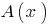 делится на многочлен
делится на многочлен  з остачею, если можно найти пару многочленов
з остачею, если можно найти пару многочленов 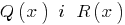 , что
, что 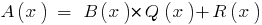 , причем степень остатка
, причем степень остатка 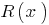 меньше степени
меньше степени  .
.
Если остаток 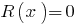 , то многочлен
, то многочлен 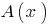 делится на многочлен
делится на многочлен  без остатка)
без остатка)
Пример
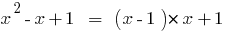
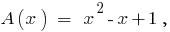
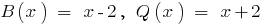
Деление многочлена на многочлен "уголком"
Правило деления многочленов от одной переменной
- Разместить члены многочленов с нисходящими степенями переменной.
- Разделить старший член делимого на старший член делителя.
- Полученный результат умножить на делитель и это произведение вычесть из делимого.
- С полученной разницей выполняют аналогичную операцию: делят ее старший член на старший член делителя и полученный результат вновь умножают на делитель и так далее. Этот процесс продолжают дать, пока не получат остатка в ноль (если один многочлен делится на другой) или пока у остатка не получат многочлен, степень которого меньше степени делителя.
Теорема Непре
Остаток от деления многочлена  на двочлен
на двочлен 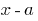 равна
равна 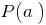
Следствие: Если 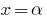 — корень многочлена
— корень многочлена  (то есть
(то есть 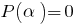 ), то этот многочлен делится без остатка на
), то этот многочлен делится без остатка на 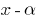 .
.
Пример
Остаток от деления многочлена 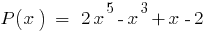 на двочлен
на двочлен 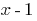 равна
равна 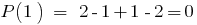 , то есть
, то есть  делится на
делится на 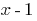 без остатка.
без остатка.
Поделив  на
на 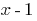 "уголком" или по схеме Горнера, получаем:
"уголком" или по схеме Горнера, получаем: 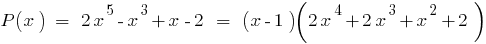

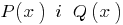 тождественно равны (то есть приобретают одинаковые значения при всех значениях
тождественно равны (то есть приобретают одинаковые значения при всех значениях