Определение: Целое число  делится на целое число
делится на целое число  , если существует такое число
, если существует такое число 
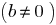 , что
, что 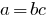 .
.
Число  называется делителем числа
называется делителем числа  , а число
, а число  — кратным числу
— кратным числу  .
.
Свойства делимости
- Если
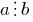 и
и 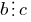 , то
, то 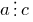 .
. - Если
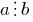 и
и 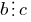 ,
,  и
и  — любые целые числа, то
— любые целые числа, то 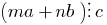 .
. - Если
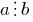 и
и 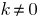 то
то 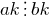 .
. - Если
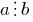 и
и 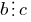 , тогда
, тогда  и
и 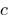 — взаємопрості числа.
— взаємопрості числа.
Признаки делимости
Признак делимости числа 2
Последняя цифра числа делится на 2 (четное).
Целое число  , что делится на 2, называется четным, и его можно представить в виде
, что делится на 2, называется четным, и его можно представить в виде 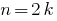 , где
, где 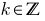 .
.
Целое число  , которое не делится на 2, называют нечетным, и его можно представить в виде
, которое не делится на 2, называют нечетным, и его можно представить в виде 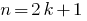 , где
, где 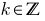 .
.
Признак делимости числа на 3
Сумма цифр числа делится на 3.
Например, число 822. Оно не содержит тройки, однако сумма его цифр: 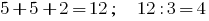 делится на 3 нацело, следовательно по признакам делимости 822 делится на 3
делится на 3 нацело, следовательно по признакам делимости 822 делится на 3 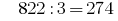 .
.
Признак делимости числа 10
Число оканчивается на 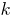 нулей.
нулей.
Признак делимости числа 4
Число, выраженное двумя последними цифрами данного числа, делится на 4.
Например, число 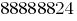 достаточно большое для деления в столбик школьниками в 7 классе.
достаточно большое для деления в столбик школьниками в 7 классе.
Однако потрібноо только проверить делимость на 4 двух последних цифр 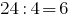 мы можем сделать вывод, что 88888824 имеет делителем четверку.
мы можем сделать вывод, что 88888824 имеет делителем четверку.
Признак делимости числа на 7
Правило делимости на 7 больших чисел. Число мысленно разбивают на блоки по три цифры, начиная с последней цифры. Согласно правила, если разница суммы блоков, стоящих на четных местах, и суммы блоков, стоящих на нечетных местах, делится на 7, то число делится на 7.
Например, 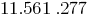
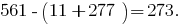
Проверим 273 по правилу
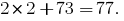
Это число "красиво" делится на 7. Таким проверить делимость числа на 7 и решить пример имеем возможность за несколькими правилами. Каждое из них имеет для ряда чисел определенные преимущества над другим, поэтому выбирайте, какой способ для Вас более понятен и быстрее.
Признак делимости числа 5
Последняя цифра числа равна 0 или 5.
Признак делимости числа 8
Число, выраженное тремя последними цифрами данного числа, делится на 8.
Признак делимости числа на 9
Сумма цифр числа делится на 9.
Признак делимости числа на 11
Разница между суммой цифр, стоящих на нечетных местах (считая справа налево), и суммой цифр, стоящих на четных местах (считая справа налево), делится на 11.

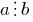 и
и 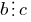 , то
, то 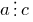 .
. и
и 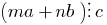 .
.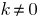 то
то 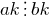 .
.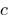 — взаємопрості числа.
— взаємопрості числа.