Понятие обратной функции: Пусть функция  принимает каждое свое значение в единственной точке ее области определения (такая функция называется обратимой ). Тогда для каждого числа
принимает каждое свое значение в единственной точке ее области определения (такая функция называется обратимой ). Тогда для каждого числа  ( из множества значений функции
( из множества значений функции  ) существует единственное значение
) существует единственное значение  (из области определения функции
(из области определения функции  ), такое, что,
), такое, что, 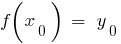 . Рассмотрим новую функцию
. Рассмотрим новую функцию 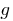 , которая каждому числу
, которая каждому числу  ставит в соответствие число
ставит в соответствие число  , то есть
, то есть 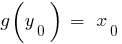 . В этом случае функция
. В этом случае функция 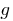 называется обратной к функции
называется обратной к функции  .
.
Свойства обратной функции
- Область определения прямой функции является множеством значений обратной, а множество значений прямой функции - область определения обратной.
- Если функция возрастает (убывает) на некотором интервале, то она имеет обратную функцию на этом интервале, которая растет, если прямая функция возрастает, и убывает, если прямая функция приходит.
- Графики прямой и обратной функции симметричны относительно прямой
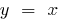 (биссектрисы первого и третьего координатных углов)
(биссектрисы первого и третьего координатных углов)
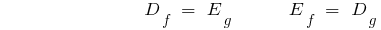
Примеры обратных функций
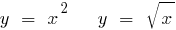
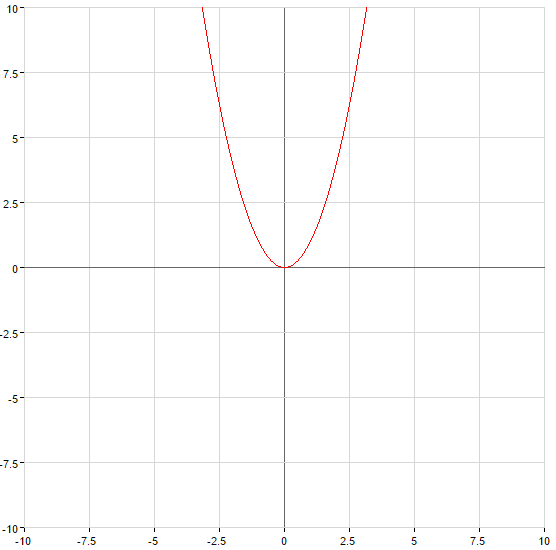
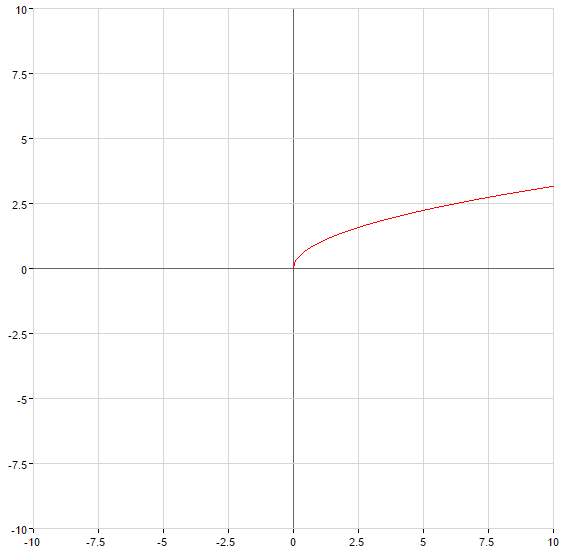
Пример нахождение обратной функции
Пример: Найти обратную функцию для функции: 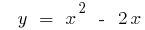
Решению: Найдем где заданная функция возрастает и убывает, 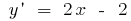 . Тогда
. Тогда 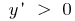 при
при 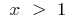 функция возрастает
функция возрастает 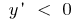 при
при 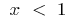 функция убывает.
функция убывает.
На каждом из этих промежутков 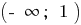 и
и 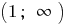 запишем формулу обратной функции. Поскольку
запишем формулу обратной функции. Поскольку 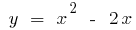 , то
, то 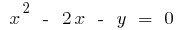 .
.
Отсюда 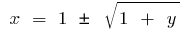 , то есть при
, то есть при 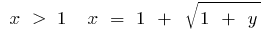 , а при
, а при 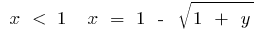 . Изменяя обозначения на традиционное, получаем: для функции
. Изменяя обозначения на традиционное, получаем: для функции 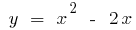 при
при 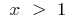 обратной функцией будет функция
обратной функцией будет функция 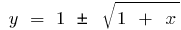 , а при
, а при 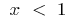 обратной функцией будет функция
обратной функцией будет функция 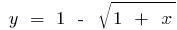 .
.

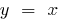 (биссектрисы первого и третьего координатных углов)
(биссектрисы первого и третьего координатных углов)