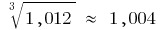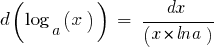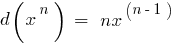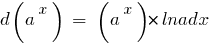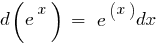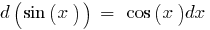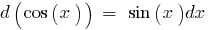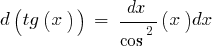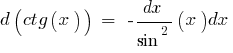Понятие дифференциала
Определение: Дифференциалом функции 
в точке 
называется произведение производной 
в этой точке, то есть 
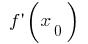на прирост аргумента 
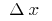(обозначается 
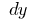или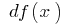 
— читается "дэ игрек")
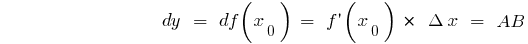
Для любой точки 
: 
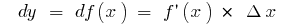если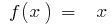 
, имеем 
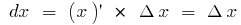, тогда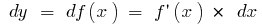 
Таблица дифференциалов элементарных функций:
Пример нахождения дифференциала в математике:
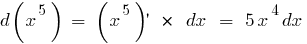
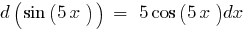
Основное свойство дифференциала
Дифференциал функции-главная линейная (то есть пропорциональная 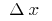) часть приращения функции
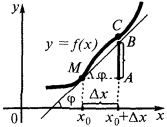
Нахождение дифференциала. Геометрический смысл дифференциала.
Правила нахождения дифференциала остаются теми же, что и для нахождения производной, нужно только умножить производную на dх.
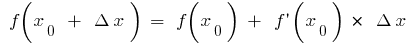
Если в формуле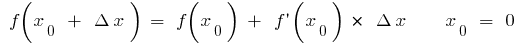 
(когда существуют 
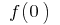и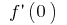 
), то для малых 
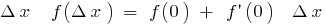. Обозначим 
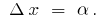Тогда для малых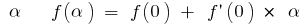 
Например:
а) для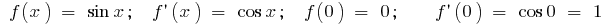 
, то есть 
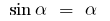(для малых 
) ;
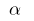б) для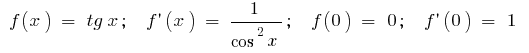 
, то есть 
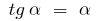(для малых )
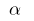Пример вычисления дифференциалов Для приближенного вычисления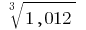 
возьмем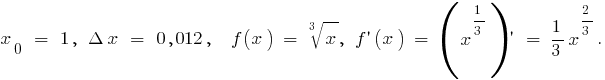 
Тогда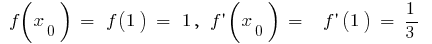 
и формула 
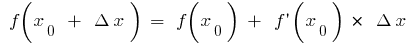дает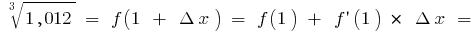 
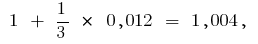то есть 