Определение: Число 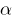 называется корнем многочлена
называется корнем многочлена  , если
, если 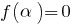 (т. е.
(т. е. 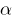 является корнем уравнения
является корнем уравнения  )
)
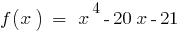 . Число 3 — корень многочлена, поскольку
. Число 3 — корень многочлена, поскольку 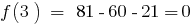
Простейшие свойства корней
- Если число
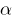 является корнем многочлена
является корнем многочлена  , то этот многочлен делится на двочлен
, то этот многочлен делится на двочлен 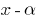 без остатка — следствие из теоремы Bézout;
без остатка — следствие из теоремы Bézout; - Многочлен степени
 может иметь не более
может иметь не более  корней;
корней; - Если для многочлена
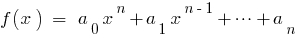 ит знаем
ит знаем  его корней:
его корней: 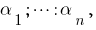 то этот многочлен можно разложить на множители так:
то этот многочлен можно разложить на множители так: 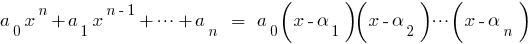 .
.
Поскольку 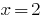 — корень многочлена
— корень многочлена 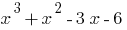 , то этот многочлен делится на
, то этот многочлен делится на 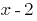 ;
;
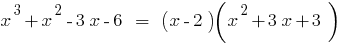
Формулы Виета
Если 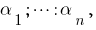 — корни многочлена
— корни многочлена 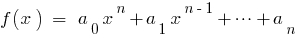 то сравнивая коэффициенты при одинаковых степенях
то сравнивая коэффициенты при одинаковых степенях  слева и справа, получаем соотношение между корнями многочлена и его коэффициентами, которые называются формулы Вієти.
слева и справа, получаем соотношение между корнями многочлена и его коэффициентами, которые называются формулы Вієти.
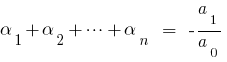
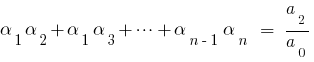
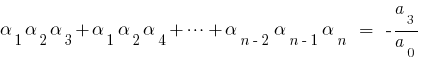
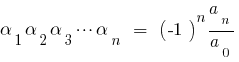
При 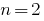 для квадратного трехчлена
для квадратного трехчлена 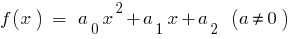 имеем
имеем
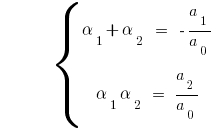
При 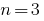 для кубического трехчлена
для кубического трехчлена 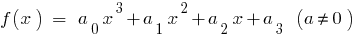 имеем
имеем
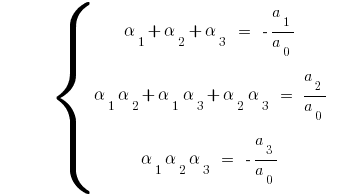

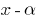 без остатка — следствие из
без остатка — следствие из  может иметь не более
может иметь не более 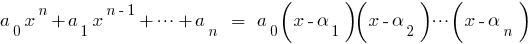 .
.