Предел функции в бесконечности

Определение: Пусть функция определена на всей числовой прямой. Число 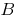называется пределом функции при 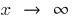, если для любого 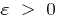найдется такое число 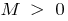, что для всех , удовлетворяющих условию 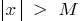, выполняется неравенство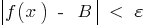

При 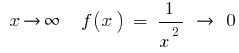, то есть при больших (по модулю) значениях число 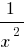очень мало отличается от числа 0

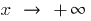Если поведение функции различна при и при 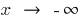, то отдельно рассматривают 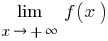(в определении берут 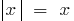) и 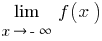(в определении берут )

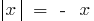Предел последовательности

Поскольку последовательность является функцией натурального аргумента 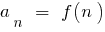, то определение предела последовательности при 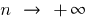вполне совпадает с определением предела функции при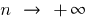

Определение: Число 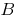называется пределом последовательности 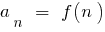, если для любого 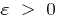существует такое число 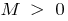, что для всех 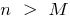, выполняется неравенство 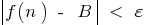т. е.

Если при 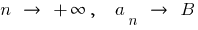, то

Сравнение роста показательной, степенной и логарифмической функций

При

,

то есть

Если , то при 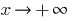функция 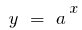растет быстрее любой степенной функции 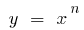, где — натуральное число

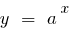Графически это утверждение означает, что при достаточно больших значениях график функции (где 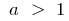) расположен выше графика функции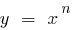

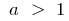
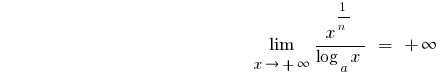При

,

то есть

,

При больших ;

,

поэтому

Если , то функция 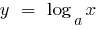возрастает медленнее, чем функция 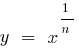(и тем более медленнее, чем функция 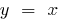или функция )

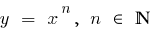Графически это утверждение означает, что при достаточно больших значениях график функции 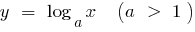расположен ниже графика функции 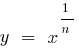(и тем более ниже графиков функций )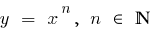