Определение: Асимптота кривой — это прямая, к которой неограниченно приближается кривая при удалении ii в нескінечність.
Вертикальные асимптоты 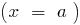
 — вертикальная асимптота,
— вертикальная асимптота,  при
при 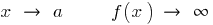
Вертикальная асимптота  может быть в точке
может быть в точке  , если точка
, если точка  ограничивает открытые промежутки области определения данной функции и у точки
ограничивает открытые промежутки области определения данной функции и у точки  функция стремится к бесконечности.
функция стремится к бесконечности.
Примеры вертикальных асимптот
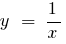
При 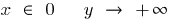
При 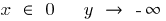
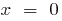 — вертикальная асимптота
— вертикальная асимптота
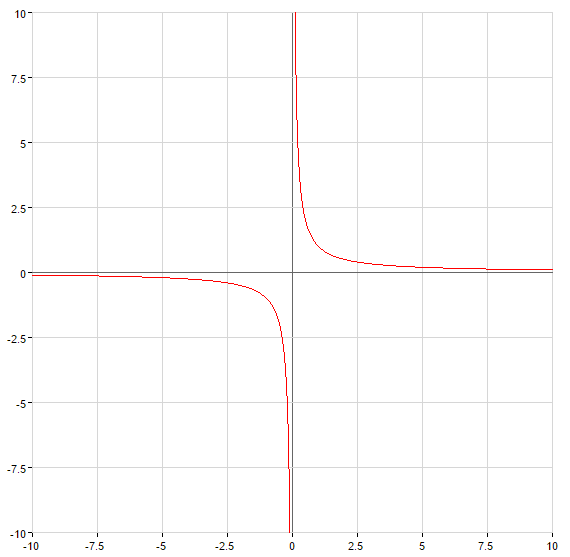
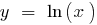
При 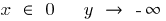
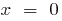 — вертикальная асимптота
— вертикальная асимптота
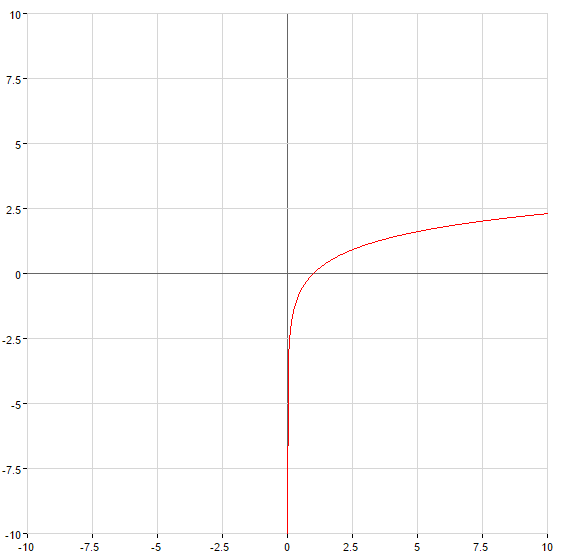
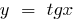
При 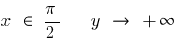
При 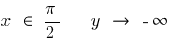
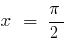 — вертикальная асимптота
— вертикальная асимптота
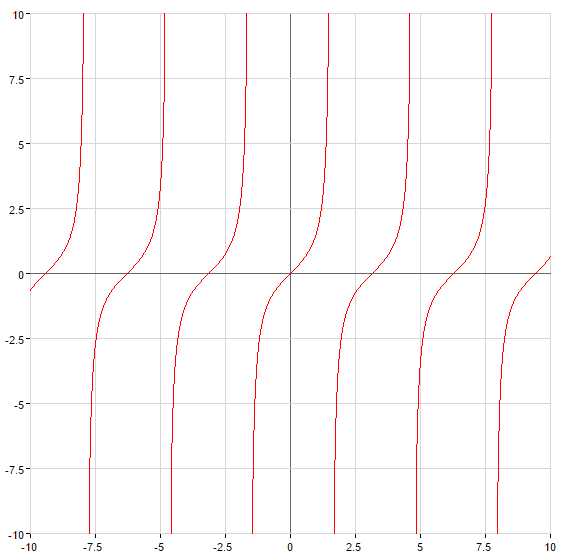
Наклонные и горизонтальные асимптоты 
- Если
 — дробно-рациональная функция, в которой степень числителя на единицу больше степени знаменателя, то выделяем целую часть и используем определение асимптоты.
— дробно-рациональная функция, в которой степень числителя на единицу больше степени знаменателя, то выделяем целую часть и используем определение асимптоты. - В общем случае уравнения наклонных и горизонтальных асимптот
 могут быть получены с использованием формул
могут быть получены с использованием формул


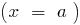
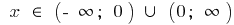
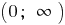
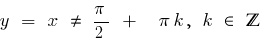

 — дробно-рациональная функция, в которой степень числителя на единицу больше степени знаменателя, то выделяем целую часть и используем определение асимптоты.
— дробно-рациональная функция, в которой степень числителя на единицу больше степени знаменателя, то выделяем целую часть и используем определение асимптоты.