Понятие второй производной



Пусть функция  имеет производную
имеет производную  во всех точках некоторого промежутка. Эта производная, в свою очередь, является функцией от
во всех точках некоторого промежутка. Эта производная, в свою очередь, является функцией от 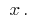 Если функция
Если функция  является дифференцированной, то ее производную называют второй производной
является дифференцированной, то ее производную называют второй производной  и обозначают
и обозначают 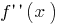 (или
(или 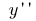 )
)
Пример. 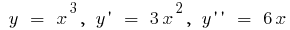
Понятие выпуклости, вогнутости и точек перегиба графика функцї
Пусть функция  определена на промежутке
определена на промежутке 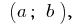 а в точке
а в точке 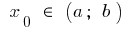 имеет конечную производную. Тогда к графику этой функции в точке
имеет конечную производную. Тогда к графику этой функции в точке 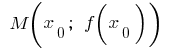 можно провести касательную
можно провести касательную
Если в некоторой окрестности точки  все точки кривой графика функции
все точки кривой графика функции  (кроме самой точки
(кроме самой точки 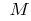 ) лежат выше касательной, то говорят, что кривая (и сама функция) в точке
) лежат выше касательной, то говорят, что кривая (и сама функция) в точке  является выпуклой (точнее, строго выпуклой). Также иногда говорят, что в этом случае график функции
является выпуклой (точнее, строго выпуклой). Также иногда говорят, что в этом случае график функции  обращен выпуклостью вниз
обращен выпуклостью вниз
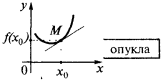
Если в некоторой окрестности точки  все точки кривой (кроме самой точки
все точки кривой (кроме самой точки  ) лежат ниже касательной, то говорят, что кривая (и сама функция) в точке
) лежат ниже касательной, то говорят, что кривая (и сама функция) в точке  является угнутою (точнее, строго угнутою). Также иногда говорят, что в этом случае график функции обращен выпуклостью вверх
является угнутою (точнее, строго угнутою). Также иногда говорят, что в этом случае график функции обращен выпуклостью вверх
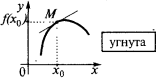
Если точка  на оси абсцисс имеет то свойство, что при переходе аргумента
на оси абсцисс имеет то свойство, что при переходе аргумента  через нее кривая
через нее кривая  переходит с одной стороны касательной на другую, то точка
переходит с одной стороны касательной на другую, то точка  называется точкой перегиба функции
называется точкой перегиба функции 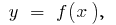 точка кривой
точка кривой 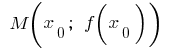 — точкой перегиба графика функции
— точкой перегиба графика функции 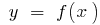
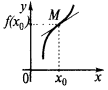
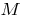 — точка перегиба графика функции
— точка перегиба графика функции
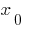 — точка перегиба функции
— точка перегиба функции
В некоторой окрестности точки  : при
: при 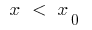 кривая ниже касательной, а при
кривая ниже касательной, а при 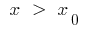 кривая выше касательной (или наоборот)
кривая выше касательной (или наоборот)
Исследование функции на выпуклость, угнутість и точки перегиба
Пример. 
- Найти область определения и интервалы, на которых функция непрерывна
- Найти вторую производную
- Найти внутренние точки области определения, в которых
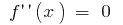 или не существует
или не существует - Отметить полученные точки на области определения, найти знак второй производной и характер поведения функции на каждом интервале, на которые разбивается область определения
- Записать нужный результат исследования (интервалы выпуклости и вогнутости и точки перегиба)
Область определения: 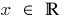
Функция непрерывная в каждой точке своей области определения
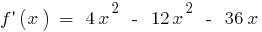
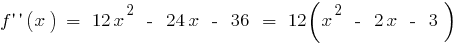
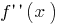 существует на всей области определения
существует на всей области определения
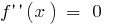 при
при 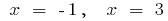
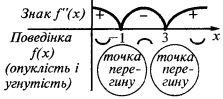
В интервале 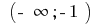 и в интервале
и в интервале 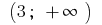 график функции
график функции  направлено выпуклостью вниз
направлено выпуклостью вниз 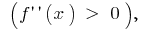 а в интервале
а в интервале  график функции
график функции  направлен выпуклостью вверх
направлен выпуклостью вверх 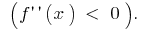
Точки перегиба: 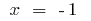 i
i 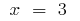 (в этих точках
(в этих точках 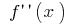 меняет знак)
меняет знак)

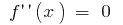 или не существует
или не существует