مفهوم المشتقة الثانية



لنفترض وظيفة  لديها المشتقة
لديها المشتقة  في كل نقطة من بعض الفاصل. هذا مشتق بدوره دالة
في كل نقطة من بعض الفاصل. هذا مشتق بدوره دالة 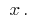 إذا كانت وظيفة
إذا كانت وظيفة  متباينة ، مشتق يسمى المشتقة الثانية
متباينة ، مشتق يسمى المشتقة الثانية  ويرمز له
ويرمز له 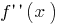 (أو
(أو 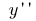 )
)
على سبيل المثال. 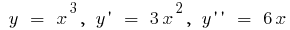
مفهوم التحدب ، التقعر ونقاط تصريف الرسم البياني funct
تسمح وظيفة  محددة على الفاصل الزمني
محددة على الفاصل الزمني 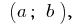 و في نقطة
و في نقطة 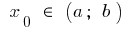 وقد محدود مشتق. ثم جدولة هذه الدالة عند نقطة
وقد محدود مشتق. ثم جدولة هذه الدالة عند نقطة 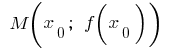 يمكن أن تعقد الظل
يمكن أن تعقد الظل
إذا كان في بعض الحي من نقطة  كل نقطة من المنحنى البياني للدالة
كل نقطة من المنحنى البياني للدالة  (باستثناء نقطة
(باستثناء نقطة 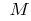 ) تقع فوق خط المماس ، ثم نقول أن منحنى (وظيفة) في نقطة
) تقع فوق خط المماس ، ثم نقول أن منحنى (وظيفة) في نقطة  محدب (أكثر دقة بدقة محدب). كما يقال في بعض الأحيان إن في هذه الحالة وظيفة الرسم البياني
محدب (أكثر دقة بدقة محدب). كما يقال في بعض الأحيان إن في هذه الحالة وظيفة الرسم البياني  هو محدب إلى أسفل
هو محدب إلى أسفل
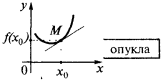
إذا كان في بعض الحي من نقطة  كل نقطة من منحنى (باستثناء نقطة
كل نقطة من منحنى (باستثناء نقطة 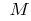 ) تقع تحت الظل ، ثم نقول أن منحنى (وظيفة) في هذه النقطة
) تقع تحت الظل ، ثم نقول أن منحنى (وظيفة) في هذه النقطة  هو potou (أو بالأحرى بدقة potou). كما يقال في بعض الأحيان إن في هذه الحالة وظيفة الرسم البياني هو محدب حتى
هو potou (أو بالأحرى بدقة potou). كما يقال في بعض الأحيان إن في هذه الحالة وظيفة الرسم البياني هو محدب حتى
إذا كانت النقطة  على محور x يحتوي على خاصية أنه إذا كانت الحجة
على محور x يحتوي على خاصية أنه إذا كانت الحجة  من خلال منحنى
من خلال منحنى  يمر من جانب واحد إلى الآخر الظل ، ثم نقطة
يمر من جانب واحد إلى الآخر الظل ، ثم نقطة  تسمى نقطة انعطاف وظيفة
تسمى نقطة انعطاف وظيفة  نقطة منحنى
نقطة منحنى 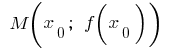 نقطة انعطاف منحنى دالة
نقطة انعطاف منحنى دالة 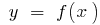
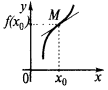
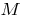 نقطة انعطاف منحنى دالة
نقطة انعطاف منحنى دالة
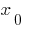 نقطة انعطاف وظيفة
نقطة انعطاف وظيفة
في بعض الأحياء من نقطة  : عندما
: عندما 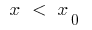 المنحنى تحت الظل ، وعندما
المنحنى تحت الظل ، وعندما 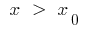 المنحنى فوق المماس (أو العكس بالعكس)
المنحنى فوق المماس (أو العكس بالعكس)
دراسة وظيفة انتفاخ ، unott و نقطة انعطاف
على سبيل المثال. 
نطاق: 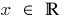
الدالة مستمرة عند كل نقطة من المجال التعريف
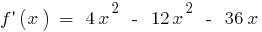
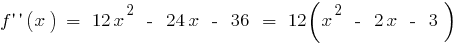
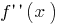 هناك في كامل نطاق
هناك في كامل نطاق
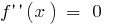 عندما
عندما 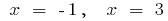
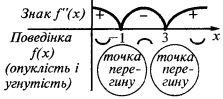
في الفاصل 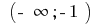 والفاصل الزمني
والفاصل الزمني 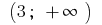 البياني للدالة
البياني للدالة  التحدب توجه إلى أسفل
التحدب توجه إلى أسفل 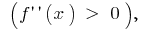 و في الفاصل الزمني
و في الفاصل الزمني  الرسم البياني للدالة
الرسم البياني للدالة  أرسلت يرفعه
أرسلت يرفعه 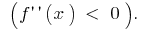
نقطة انعطاف: 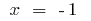 أنا
أنا 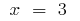 (في هذه النقاط
(في هذه النقاط 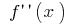 التغييرات علامة)
التغييرات علامة)
- للعثور على نطاق و على فترات على وظيفة مستمر
- إيجاد المشتقة الثانية
- العثور على نقطة داخلية من تحديد مكان
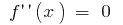 أو ليس هناك
أو ليس هناك - مارك الناتجة نقطة على نطاق العثور على إشارة المشتقة الثانية و سلوك الدالة على كل الفاصل الذي يقسم تعريف المنطقة
- لتسجيل النتيجة المرجوة من الدراسة (فترات التحدب و التقعر و نقطة انعطاف)

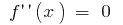 أو ليس هناك
أو ليس هناك