这一概念的第二衍生物



假定能  有一个衍生物
有一个衍生物  的所有点的一些时间间隔。 这一衍生物,又是一个函数
的所有点的一些时间间隔。 这一衍生物,又是一个函数 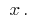 ,如果功能
,如果功能  是有区别的,其衍生物是所谓的第二衍生物
是有区别的,其衍生物是所谓的第二衍生物  和记
和记 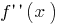 (或
(或 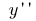 )
)
例。 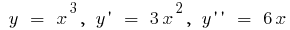
概念凸,凹面和拐点的图表功能
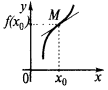
让我们功能  上定义的时间间隔
上定义的时间间隔 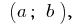 ,并在点
,并在点 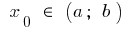 具有有限的衍生物。 然后安排这种功能在这点
具有有限的衍生物。 然后安排这种功能在这点 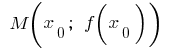 可以保持 切
可以保持 切
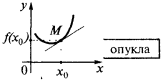
如果在一些邻居点  的所有各点的曲线的函数的曲线图
的所有各点的曲线的函数的曲线图  的(除分
的(除分 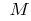 )的谎言上的切线,那么我们说,曲线(如功能)点
)的谎言上的切线,那么我们说,曲线(如功能)点  是凸(更确切地说,严格凸). 此外,它们有时说,在这种情况下的函数的曲线图
是凸(更确切地说,严格凸). 此外,它们有时说,在这种情况下的函数的曲线图  ,是凸下
,是凸下
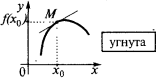
如果在一些邻居点  的所有各点的曲线(除了一点
的所有各点的曲线(除了一点  )躺下切,然后我们说的曲线(如功能)点
)躺下切,然后我们说的曲线(如功能)点  是potou(或者说,严格potou). 此外,它们有时说,在这种情况下的函数的曲线图,是凸起
是potou(或者说,严格potou). 此外,它们有时说,在这种情况下的函数的曲线图,是凸起
如果点是  在x轴上有该财产,如果参数
在x轴上有该财产,如果参数  通过曲线
通过曲线  从一个侧面切,然后点
从一个侧面切,然后点  是所谓的转折点的功能
是所谓的转折点的功能 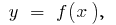 点的曲线
点的曲线 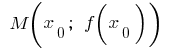 点的拐的一个函数的曲线图
点的拐的一个函数的曲线图 
 的拐点的一个函数的曲线图
的拐点的一个函数的曲线图
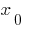 拐点的功能
拐点的功能
在一些邻居的一点  :当
:当 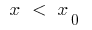 的曲线是下面的切,并且当
的曲线是下面的切,并且当 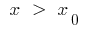 的曲线之上的切(或反之亦然)
的曲线之上的切(或反之亦然)
研究功能的隆起,unott和拐点
例。 
范围: 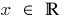
该职能是连续的每一点域的定义
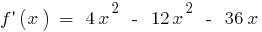
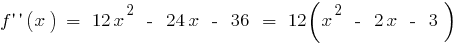
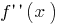 存在的整个范围
存在的整个范围
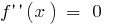 时
时 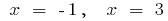
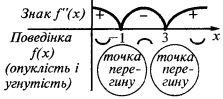
在间隔 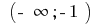 和间隔
和间隔 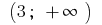 的函数的曲线图
的函数的曲线图  凸指导下
凸指导下 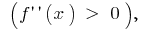 和在区间
和在区间  的函数的曲线图
的函数的曲线图  发给撞了
发给撞了 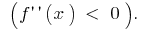
拐点: 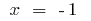 i
i 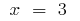 (在这些点
(在这些点 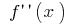 的变化的迹象)
的变化的迹象)
- 找到 的范围 和间隔的功能是连续的
- 找到第二衍生物
- 找到一点内部的确定
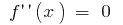 或不存在的
或不存在的 - 标记得点的范围,找到标志的第二衍生物和行为的功能,在每个时间间隔,分区域的定义
- 来记录所期望的结果的研究(间隔凸和凹度和拐点)

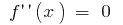 或不存在的
或不存在的