这一概念的系统及其rozvytku
定义: 如果任务是找到所有共同的解决方案的两个(或更多)方程式的一个或多个变量,那么我们就说,这是必要的 razvesti系统 的方程式。
定义: Rozvyazka系统 的价值变量或诸如定购置的价值观smya,满足所有的方程式的系统,即rozvyazka系统的两个或多个方程式与  未呼吁这样一个有序的设置一个很大
未呼吁这样一个有序的设置一个很大  的数字,后替代的其进入该系统是未知的,所有的方程变得真实的数值的平等。
的数字,后替代的其进入该系统是未知的,所有的方程变得真实的数值的平等。
定义: Razvesti系统的方程 是 找到其所有的交汇处 ,或者证明他们不是。
如果系统没有解决,那么它是不相容的。
例的系统
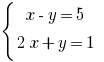 —一个系统的两个公式有两个变量
—一个系统的两个公式有两个变量
对 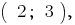 这就是
这就是 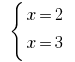 一个解决方案的系统
一个解决方案的系统
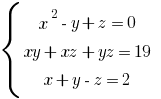 —该系统的三个方程式与三个变量
—该系统的三个方程式与三个变量
三个 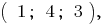 也就是
也就是 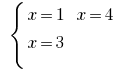 一个rozvytku系统
一个rozvytku系统
方案的解决方案方程组
图形的方法
- 执行同等的变革,所以,很方便地图的功能。 例如:
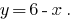
- 建立的图形。
- 找到交汇点的图表。 这些座标点是rozvyazka这种系统的方程式。
该替代方法
- 一个公式的系统中,我们表达的一个变量经另一个的,总是选择便利的变量。 例如,从该方程式
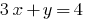 我们表示的变量
我们表示的变量 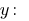
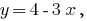 ,而不是相反。
,而不是相反。 - 替代品的价值的发现进入另一个公式的系统和获得一个等式的一个变量。
- Rozvadov的衍生的公式
- 找到的值被取代的表述方程式,并找到的价值第二个变量。
添加的方法
- Urunov系数的一个变量过期的乘法运算的这两个方程上的乘数,相应地选择。
- 添加(或减去)pocino两个方程式系统,从而消除了一个变量。
- Rozvadov得到的公式。
- 替代发现的价值变量中的任何原有的方程式。
实例的解决系统的方程
方案通过图形的方法
例1
Rozwarte方程式: 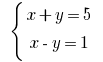
方案:
建立的图形 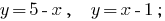
建设图形看到,图相交的点 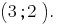
回答: 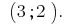
决定的方法的替代
例2
Rozwarte方程式: 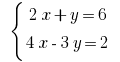
方案:
从第一个方程式我们表示 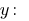
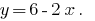 ,替代品得到表达成的第二个等式的系统:
,替代品得到表达成的第二个等式的系统:
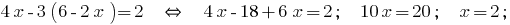
得到的数值  代入表达式
代入表达式 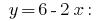
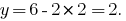
回答: 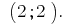
解决方案,通过添加
例3
Rozwarte方程式: 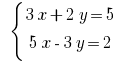
方案:
需要摆脱的一个变量 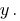 poslano乘的第一个公式的系统3和第二次2。
poslano乘的第一个公式的系统3和第二次2。
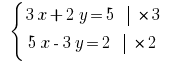
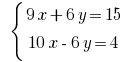
添加pocino式和获得: 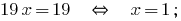
找到价值  的第一个公式的系统:
的第一个公式的系统: 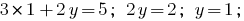
回答: 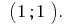
注: 方法增加,可以成倍增加,不仅在正数和负数。
如何rozwiazywanie系统的方程式来解决只有你。

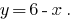
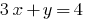 我们表示的变量
我们表示的变量 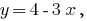 ,而不是相反。
,而不是相反。