定义: 数 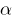 是所谓 的根源的多项式
是所谓 的根源的多项式  ,如果
,如果 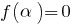 (即
(即 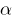 是一个根本的公式
是一个根本的公式  )
)
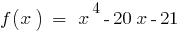 中。 数3是一个根源,因为多项式
中。 数3是一个根源,因为多项式 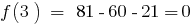
基本性根源
由于 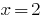 是一个根本的多项式,
是一个根本的多项式, 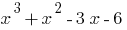 那么这多项式分为
那么这多项式分为 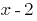 ;
;
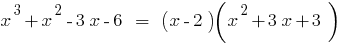
- 如果人数
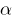 是一个根本的多项式
是一个根本的多项式  ,那么这多项式分通过迪克兰
,那么这多项式分通过迪克兰 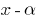 没有一个跟踪的后果 Bézout定理;
没有一个跟踪的后果 Bézout定理; - 多项式的程度
 具有最多
具有最多  根源;
根源; - 如果多项式
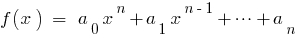 ,它知道,
,它知道,  其根源:
其根源: 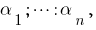 那么这多项式可以因式分解:
那么这多项式可以因式分解: 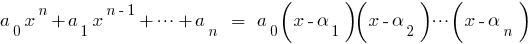 .
.
公式韦达
如果 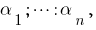 根源的多项式
根源的多项式 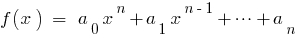 则比较系数的平等权力
则比较系数的平等权力  的左右,我们获得之间的关系的根源的多项式和系数,这是所谓的 公式WTI的。
的左右,我们获得之间的关系的根源的多项式和系数,这是所谓的 公式WTI的。
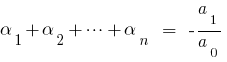
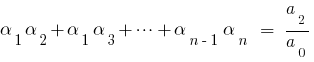
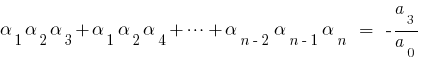
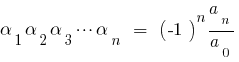
当 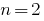 对方三项
对方三项 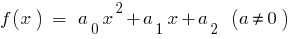 都是
都是
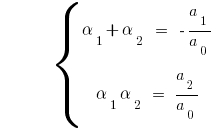
如果 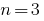 对立方的三项
对立方的三项 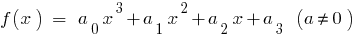 都是
都是
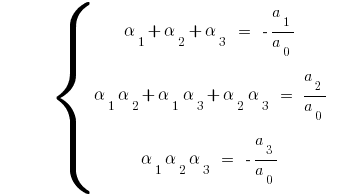

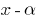 没有一个跟踪的后果
没有一个跟踪的后果  具有最多
具有最多 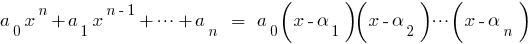 .
.