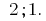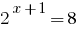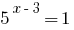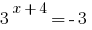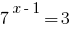支持的事实
任何增加(减少)之间的功能每个获得其价值仅在一点的这段期间。
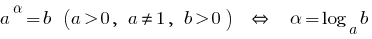
当 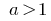 的指数函数
的指数函数  不断增加。
不断增加。
时  。
。
当 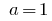 的指数函数
的指数函数  。
。
实例的解决方案的简单的指数公式
方案:
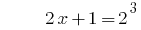
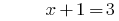
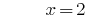
回答: 
方案:
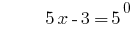
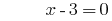
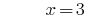
回答: 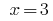
方案:
没有根(使 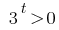 )
)
回答: 没有根
方案:
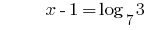
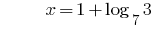
回答: 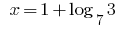
实例的解决方案方程式的模型,通过减少到最简单
______________________________________________________________________
如果左右部分方程式只是说明性的工作,分数,根AO程度,最好是使用基本的公式对试图记录的两个部分的公式为权力的一个基础。
______________________________________________________________________
实例1:
Rozwarte方程式 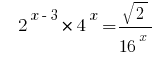 的。
的。
方案:
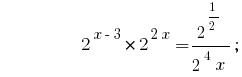
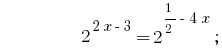
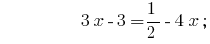
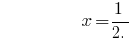
答: 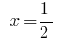 中。
中。
______________________________________________________________________
如果其中一部分的指数公式是一些和其他包含所有成员的表情 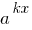 (指数不同,只有通过免费的成员),这是方便在这个等式的一部分搁置的最小的程度
(指数不同,只有通过免费的成员),这是方便在这个等式的一部分搁置的最小的程度  上。
上。
______________________________________________________________________
实例2:
Rozwarte方程式 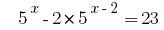 的。
的。
方案:
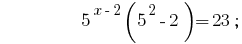
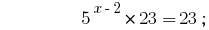
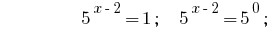
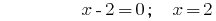
答: 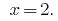 中。
中。
例更为复杂的指数公式
______________________________________________________________________
摆脱数字方面的指数 (利用右到左的基本属性 的程度).
如果可能,减少所有度的一个基础和执行变化的变量。
______________________________________________________________________
实例3:
Rozwarte方程式 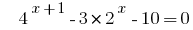 的。
的。
方案:
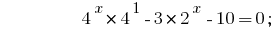
鉴于 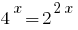 我们的降低程度的一个基2:
我们的降低程度的一个基2: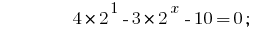
取代 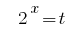 给的公式:
给的公式:
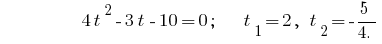
向后代提供公式 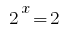 ,
,  或者
或者 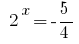 -没有根源。
-没有根源。
回答: 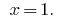
______________________________________________________________________
如果没有程度可减至一个基础,尽量减少所有度的两个基地以便获得一种 均质的等式。
______________________________________________________________________
实例4:
Rozwarte方程式 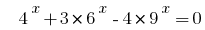 的。
的。
方案:
让我们给所有的程度的两个基2和3:
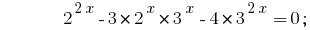
有一均质的等式。 对于它的解决方案鸿沟双方通过 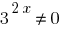 的;
的;
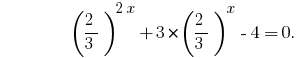
取代 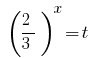 给的公式:
给的公式:
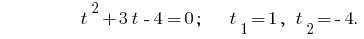
向后代提供公式 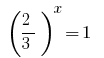 ,
, 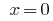 或者
或者 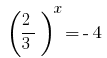 -没有根源。
-没有根源。
回答: 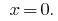
______________________________________________________________________
在其他情况下,我们转移的所有条款在这方程式纳入的一部分,并尝试来分解该得到表达成因素,或者应用特殊技术的解决方案中,我们使用的属性相应的功能。
______________________________________________________________________
例5:
Rozwarte方程式 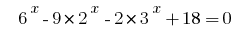 的。
的。
方案:
如果在对集团成员在左侧的公式,并在每一对站出来一个共同的因素,我们会得到:
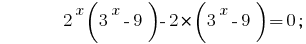
使括号内的一个共同的因素 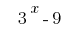 :
:
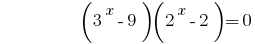
然后 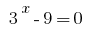 或
或 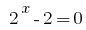 .
.
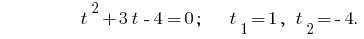
我们得到两个方程式1)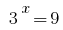 其中
其中  2)
2)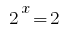 在那里
在那里  的。
的。
回答: