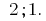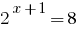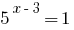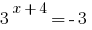समर्थन तथ्यों
किसी भी वृद्धि (कम) समारोह के बीच में से प्रत्येक में अपनी मूल्य केवल एक ही बात में इस अवधि के.
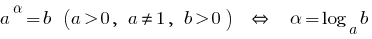
जब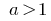 
घातीय समारोह 
बढ़ रही है ।
जब में आता है ।
जब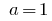 
घातीय समारोह था.
निर्णय मॉडल समीकरणों में से एक को पता होना चाहिए कि गुणों की जड़ों और डिग्री ।
उदाहरण के समाधान के सरल घातीय समीकरण
समाधान:
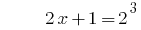
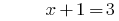
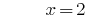
जवाब: 
समाधान:
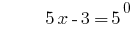
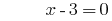
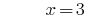
जवाब: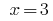 
समाधान:
कोई जड़ों (तो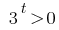 
)
जवाब: कोई जड़ों की
समाधान:
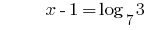
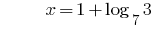
जवाब: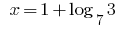 
उदाहरण के समाधान के मॉडल द्वारा समीकरणों में कमी करने के लिए सरल
______________________________________________________________________
यदि छोड़ दिया और सही भागों के समीकरण के उदाहरण हैं केवल काम की, भिन्न, जड़ों AO हद तक, यह सलाह दी जाती है का उपयोग कर के बुनियादी सूत्रों की कोशिश करने के लिए रिकॉर्ड करने के लिए दोनों समीकरण के कुछ हिस्सों के रूप में शक्तियों का एक आधार है ।
______________________________________________________________________
उदाहरण 1:
Rozwarte समीकरण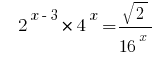 
है ।
समाधान:
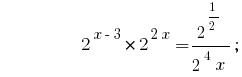
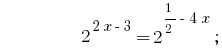
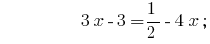
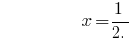
जवाब: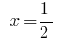 
.
______________________________________________________________________
यदि एक भाग के घातीय समीकरण है की एक संख्या और अन्य युक्त सभी सदस्यों की अभिव्यक्ति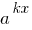 
(exponents द्वारा केवल भिन्न होते हैं नि: शुल्क सदस्य), यह सुविधाजनक है में इस समीकरण का हिस्सा डाल करने के लिए एक तरफ छोटी से छोटी डिग्री 
में.
______________________________________________________________________
उदाहरण 2:
Rozwarte समीकरण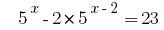 
है ।
समाधान:
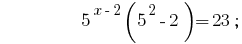
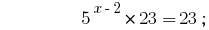
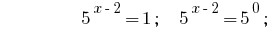
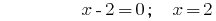
जवाब: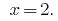 
.
उदाहरण के और अधिक जटिल घातीय समीकरण
______________________________________________________________________
से छुटकारा पाने के संख्यात्मक के संदर्भ में exponents (का उपयोग कर सही करने के लिए छोड़ दिया बुनियादी गुणों की डिग्री).
यदि संभव हो तो, सभी को कम डिग्री करने के लिए एक आधार और एक चर के परिवर्तन.
______________________________________________________________________
उदाहरण 3:
Rozwarte समीकरण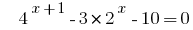 
है ।
समाधान:
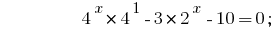
यह देखते हुए कि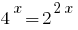 
, हम कम की डिग्री के द्वारा एक आधार 2: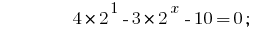
प्रतिस्थापन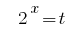 
देता है समीकरण:
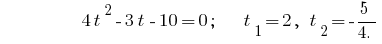
पिछड़े प्रतिस्थापन के समीकरण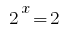 
, जहां 
या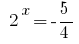 
- कोई जड़ है.
जवाब: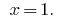 
______________________________________________________________________
नहीं तो डिग्री कम किया जा सकता है के लिए एक आधार को कम करने की कोशिश सभी डिग्री के लिए दो कुर्सियां इतनी के रूप में प्राप्त करने के लिए एक सजातीय समीकरण है.
______________________________________________________________________
उदाहरण 4:
Rozwarte समीकरण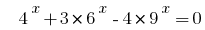 
है ।
समाधान:
चलो सभी की हद तक के लिए दो कुर्सियां 2 और 3:
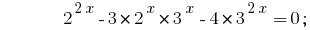
एक सजातीय समीकरण है. इसके समाधान के लिए विभाजित करके दोनों पक्षों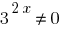 
;
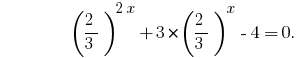
प्रतिस्थापन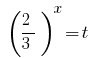 
देता है समीकरण:
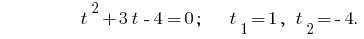
पिछड़े प्रतिस्थापन के समीकरण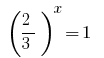 
, जहां 
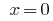या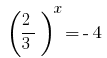 
- कोई जड़ है.
जवाब: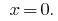 
______________________________________________________________________
अन्य मामलों में, हम सभी हस्तांतरण के मामले में समीकरण का एक हिस्सा है और कोशिश विघटित करने के लिए प्राप्त अभिव्यक्ति में कारकों, या लागू करने के लिए विशेष तकनीक में समाधान जो हम उपयोग गुण के लिए इसी का कार्य है ।
______________________________________________________________________
उदाहरण 5:
Rozwarte समीकरण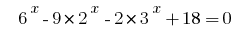 
है ।
समाधान:
यदि जोड़े में करने के लिए समूह के सदस्यों के बाईं ओर में इस समीकरण, और प्रत्येक जोड़ी में बाहर खड़े एक आम कारक है, हम प्राप्त :
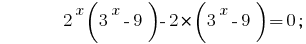
कोष्ठक बनाने के लिए एक आम कारक है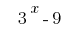 
:
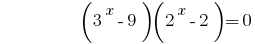
तो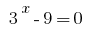 
या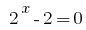 
.
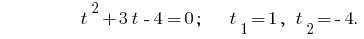
हम दो समीकरण 1)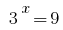
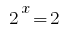जहां 2) जहां .
जवाब: 